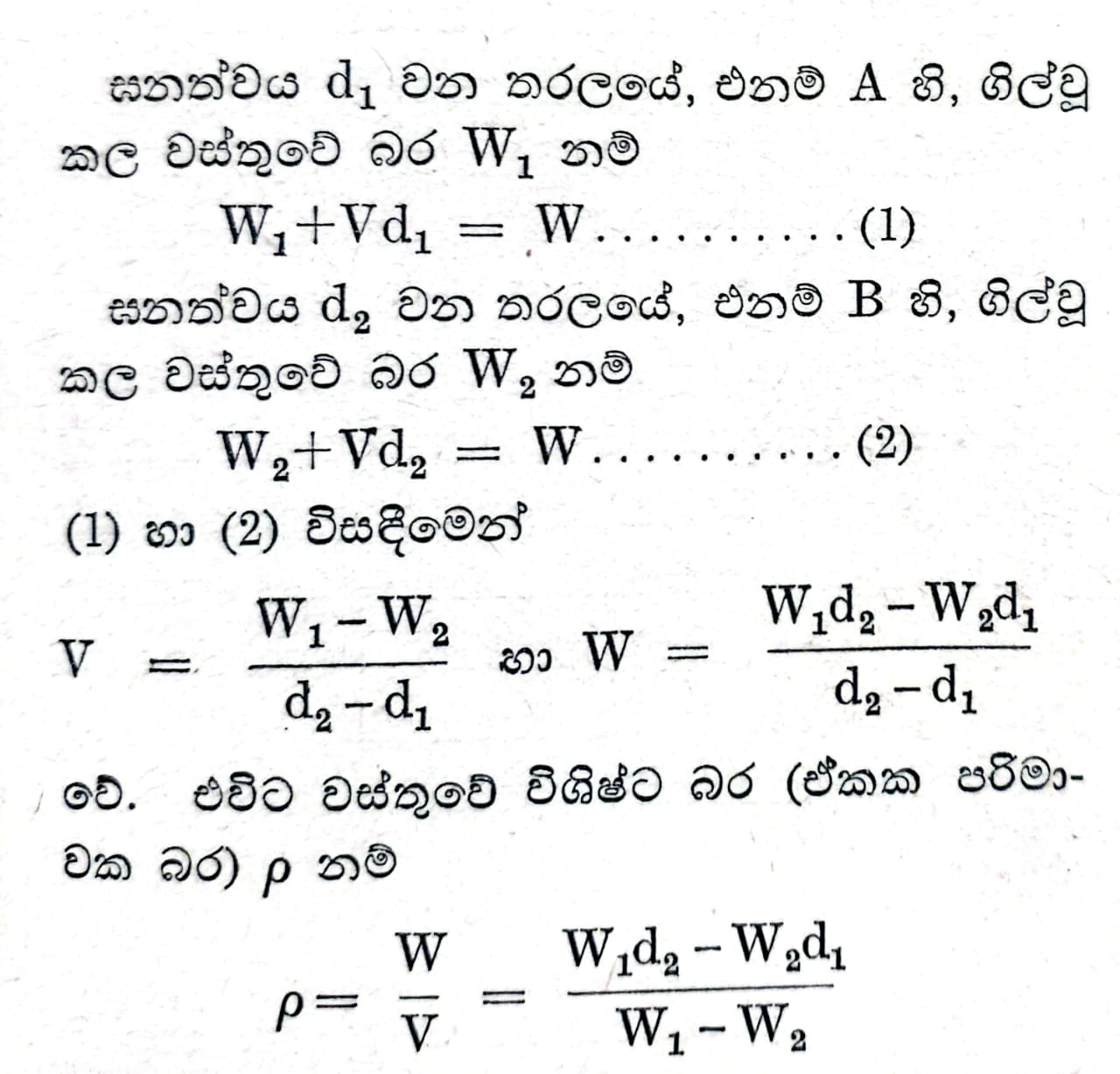ඉපිලුම් නියමය
ස්ථිතික තරලයක ගිල්වන ලද වස්තුවක් කෙරෙහි එමගින් විස්ථාපිත තරල පරිමාවට සමාන බරකින් යුත් බලයක් ක්රියා කරන අතර එම තරලයෙහි ඉපිලෙන වස්තුවක් මගින් වස්තුවේ බරට සමාන බරකින් යුත් තරල පරිමාවක් විස්ථාපනය කෙරෙන බව ආකිමිඩීස් විසින් සොයා ගන්නා ලදි. උදාහරණයක් දක්වතොත්, බැලුමක් ඉහළට නඟින්නේ බැලුමේ බරට වඩා වැඩි බරකින් යුත් වාතයේ පරිමාවක් විස්ථාපනය වන විටය. මෙම මූලධර්මය ප්රථමයෙන් ප්රකාශ කළ ආකිමිඩීස් (ක්රි.පූ. 287-212) ඔටුන්නක රත්රන් හා රිදී ප්රමාණයන් නිර්ණය කරගැනීම සඳහා එය උපයෝගී කර ගත්තේය. තරලය මඟින් වස්තුවක පහළ හා ඉහළ පෘෂ්ඨයන්හි ක්රියා කෙරෙන බලයේ සිරස් සංරචකයන්ගේ වෙනස නිර්ණය කිරීමෙන් මෙම මූලධර්මය සාධනය කළ හැකිය. උත්ප්ලාවකතා බලය නමින් හඳුන්වනු ලබන මෙම බලය තරලයේ විස්ථාපිත පරිමාවේ කේන්ද්රකය ඔස්සේ සිරස් ලෙස උඩු අතට ක්රියා කරයි.
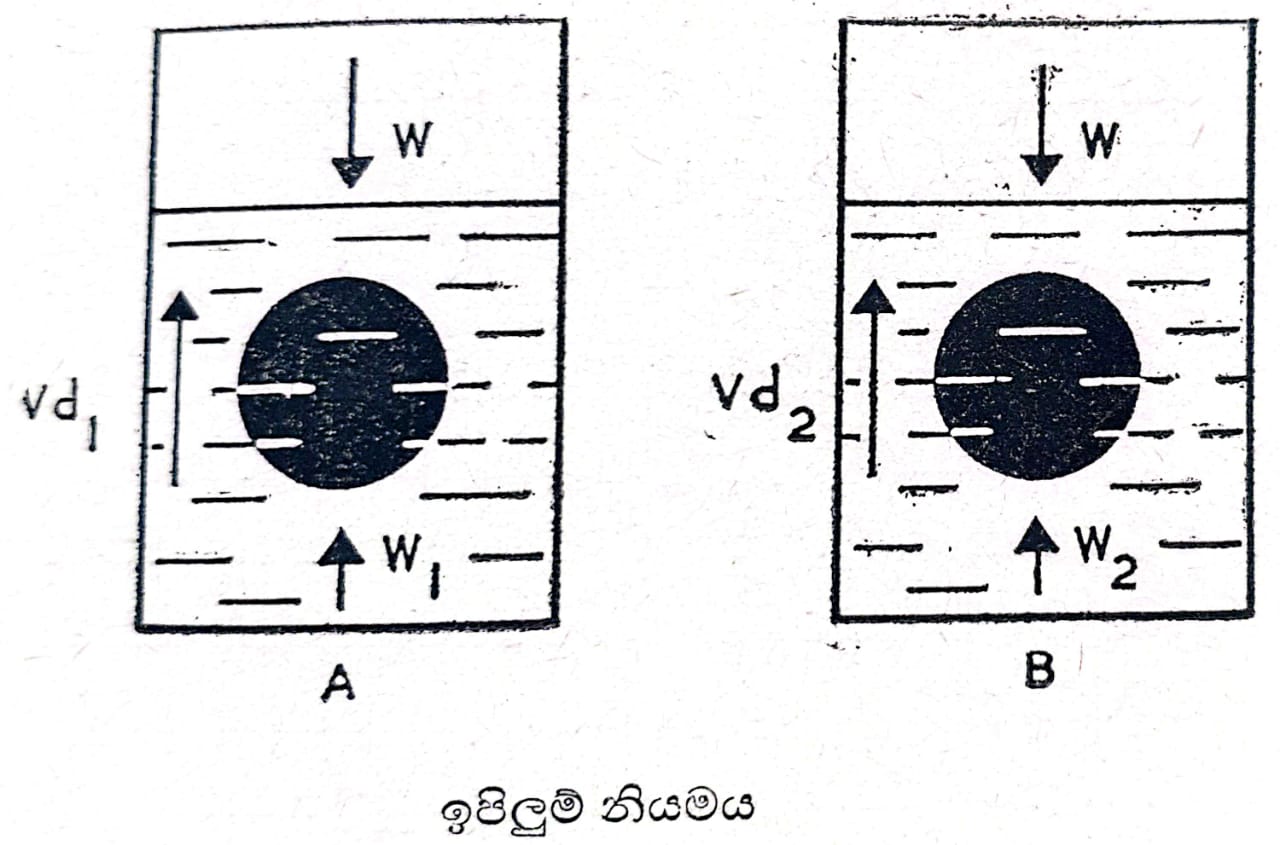
ඉපිලුම් නියමය උපයෝගී කොටගෙන වස්තුවක විශිෂ්ට බර සොයාගැනීම සඳහා එම වස්තුව ඝනත්වය d1 හා d2 වන තරල දෙකක වෙන් වෙන් වශයෙන් කිරනු ලැබේ. වස්තුවේ පරිමාව V හා එහි බර W යැයි සිතමු.
ඝනත්වය d1 වන තරලයේ, එනම් A හි, ගිල්වූ කල වස්තුවේ බර W1 නම් W1+Vd1 = W…………….(1)
ඝනත්වය d2 වන තරලයේ, එනම් B හි, ගිල්වූ කල වස්තුවේ බර W2 නම් W2+Vd2 = W…………….(2)
(1) හා (2) විසඳීමෙන් ..................................................................... වේ. එවිට වස්තුවේ විශිෂ්ට බර (ඒකක පරිමාවක බර) þ නම් ........................................................................................ වේ. තවද සම්මත තත්වයෙහි පිහිටි ජලයේ විශිෂ්ට බරින් මෙම þහි අගය බෙදීමෙන් වස්තුවේ විශිෂ්ට ගුරුත්වය, එනම් වස්තුවේ ඝනත්වය හා ජලයේ ඝනත්වය අතර අනුපාතය ලබාගත හැකිය.
ඉපිලුම් නියමයේ එක් ප්රයෝගයක් වශයෙන් ද්රවමානය උපයෝගී කොටගෙන ද්රවයක විශිෂ්ට ගුරුත්වය නිර්ණය කිරීම දැක්විය හැකිය. සිහින් කඳක් සහිත බර වස්තුවක් වන ද්රවමානය ද්රවයේ සිරස් ලෙස ඉපිලෙන සේ සකස් කර ඇත. විශිෂ්ට ගුරුත්වයට සමානුපාතික වන සේ ක්රමාංකිත පරිමාණයකින් යුත් කඳේ යම් ස්ථානයක ද්රව පෘෂ්ඨය පිහිටයි. ජලයට වඩා අඩු විශිෂ්ට ගුරුත්වයකින් යුත් ද්රවයක ද්රවමානයේ වැඩි කොටසක් ගිලෙන අතර විස්ථාපිත ද්රවයේ බර හැම විට ම එක සමාන වේ. ද්රවමානය ඒ ඒ ද්රවයේ ගිලෙන උසින් එම ද්රවවල විශිෂ්ට ගුරුත්වය කියවිය හැක. උෂ්ණත්වය අනුව විශිෂ්ට ගුරුත්වය ශීඝ්රයෙන් වෙනස් වන නිසා උෂ්ණත්ව ශෝධනයක් හෝ සම්මත උෂ්ණත්වයක දී මැනීමක් හෝ අවශ්ය වේ.
ස්ථිතික තරලයක ඉපිලෙන වස්තුවක් කෙරෙහි ක්රියා කෙරෙන සම්ප්රයුක්ත සිරස් බලය උත්ප්ලාවකතා බලය වශයෙන් හඳුන්වන බව මුලින් සඳහන් විය. මෙම බලය උඩුකුරු ලෙස සිරස්ව ක්රියා කරයි. එයට ප්රතිවිරුද්ධව ඇති බලය ගුරුත්වාකර්ෂණ බලයයි. විස්ථාපිත තරල පරිමාවේ බරට මෙම බලයේ විශාලත්වය සමාන වන අතර ක්රියා රේඛාව ද්රව පරිමාවේ කේන්ද්රකය ඔස්සේ පිහිටයි. මෙම කේන්ද්රකය උත්ප්ලාවකතා කේන්ද්රය වශයෙන් හඳුන්වනු ලැබේ.
ස්ථිතික තරලයක ඉපිලෙන වස්තුවක් සිරස් ස්ථායිතාවෙන් යුක්ත වේ. උඩු අතට යෙදූ කුඩා විස්ථාපනයක් මඟින් විස්ථාපිත තරල පරිමාව අඩු කෙරෙන බැවින් උත්ප්ලාවකතා බලය ද අඩු වෙයි. එනයින් ඇති වන සම්ප්රයුක්ත බලය ආරම්භක ස්ථානය කරා වස්තුව ආපසු ගෙන යයි. එලෙසට ම යටිකුරුව යෙදූ කුඩා විස්ථාපනයක් මගින් උත්ප්ලාවකතා බලය වැඩි කෙරෙන නිසා උඩුකුරු අතට සම්ප්රයුක්ත බලයක් ඇති කරයි.
වස්තුවක් භ්රමණ ස්ථායිතාවෙන් යුක්ත වන්නේ එම වස්තුව කෙරෙහි කුඩා කෝණික විස්ථාපනයක් යෙදූ කල එය ආරම්භක ස්ථානයට නැවත ගෙනයන පරිදි වූ ප්රතිපාදන බලයුග්මයක් ඇති කරන විටයි. ඉපිලෙන වස්තුවක උත්ප්ලාවකතා කේන්ද්රයට වඩා පහළින් ගුරුත්ව කේන්ද්රය පිහිටන විට එම වස්තුව සෑම විට ම භ්රමණ ස්ථායිතාවෙන් යුක්ත වේ. ඉපිලෙන වස්තු බොහොමයක ගුරුත්ව කේන්ද්රය පිහිටා ඇත්තේ උත්ප්ලාවකතා කේන්ද්රයට වඩා ඉහළින්ය. නැව මෙයට කදිම නිදසුනකි. වස්තුවේ හැඩය භ්රමණ ස්ථායිතාව කෙරෙහි විශේෂයෙන් බලපායි. එය සමතුලිතව ඉපිලෙන කල උත්ප්ලාවකතා කේන්ද්රය හා ගුරුත්ව කේන්ද්රය එක ම සිරස් රේඛාවේ පිහිටයි. එම වස්තුව ඇල කළ කල්හි විස්ථාපිත තරලයේ අලුත් කේන්ද්රකයට උත්ප්ලාවකතා කේන්ද්රය තැන් මාරු වන අතර උත්ප්ලාවකතා බලය එම අලුත් කේන්ද්රය ඔස්සේ සිරස්ව ක්රියා කරයි. එවිට මෙම සිරස් රේඛාව ද මුල් උත්ප්ලාවකතා කේන්ද්රය හා ගුරුත්ව කේන්ද්රය යා කරන රේඛාව ද ඡේදනය වන අතර එම ඡේදන ලක්ෂ්යය චලකේන්ද්රය වශයෙන් හඳුන්වනු ලැබේ. ඉපිලෙන වස්තුවක් භ්රමණ ස්ථායිතාවෙන් යුක්ත වන්නේ ගුරුත්ව කේන්ද්රයට ඉහළින් චලකේන්ද්රය පිහිටන විට පමණි. ගුරුත්ව කේන්ද්රය හා චලකේන්ද්රය අතර දුර චල කේන්ද්රික උස වශයෙන් හඳුන්වනු ලැබේ. එය වස්තුවේ ස්ථායිතාවේ නොවක් මිනුමකි.
(කර්තෘ: තිලක් ගුණසේකර)
(සංස්කරණය: 1970)
