"අඞ්ක ගණිතය" හි සංශෝධන අතර වෙනස්කම්
('අංක හෙවත් ඉලක්කම් මගින් ප්රකාශ කෙරෙන සංඛ්ය...' යොදමින් නව පිටුවක් තනන ලදි) |
Senasinghe (කතාබහ | දායකත්ව) |
||
| (නොපෙන්වන එම පරිශීලකයා මගින් අතරමැදි සංස්කරණ 4ක්) | |||
| 6 පේළිය: | 6 පේළිය: | ||
කවුද, කොහොමද, කොහේ ආදි ප්රශ්නවලට උත්තර දීම සඳහා මිනිසා සාමාන්ය භාෂාව යොදා ගනී. එසේ වුව ද කීය ද කොපමණ ද ආදී ප්රශ්නවලට උත්තර දීම සදහා මිනිසාට තමන්ගේ සමාන්ය භාෂාවට අමතර වශයෛන් අලුත් වචන නිපදවා ව්යවහාර කිරීමට සිදුවිය. ජිවිතයේ සියලු අවස්ථාවන්හිදී ම මේ අන්දමේ ප්රශ්න ඉදිරිපත් වන නිසා භාවිතයෙහි යෙදෙන භාෂාවට අලුත් වචන යොදාගන්ට වීමෙන් ගණිතමය භාෂාවක් ද ඇති විය. කීය ද කොපමණ ද ආදි ප්රශ්නවලට උත්තර සැපයෙන්නේ සංඛ්යා මගිනි. | කවුද, කොහොමද, කොහේ ආදි ප්රශ්නවලට උත්තර දීම සඳහා මිනිසා සාමාන්ය භාෂාව යොදා ගනී. එසේ වුව ද කීය ද කොපමණ ද ආදී ප්රශ්නවලට උත්තර දීම සදහා මිනිසාට තමන්ගේ සමාන්ය භාෂාවට අමතර වශයෛන් අලුත් වචන නිපදවා ව්යවහාර කිරීමට සිදුවිය. ජිවිතයේ සියලු අවස්ථාවන්හිදී ම මේ අන්දමේ ප්රශ්න ඉදිරිපත් වන නිසා භාවිතයෙහි යෙදෙන භාෂාවට අලුත් වචන යොදාගන්ට වීමෙන් ගණිතමය භාෂාවක් ද ඇති විය. කීය ද කොපමණ ද ආදි ප්රශ්නවලට උත්තර සැපයෙන්නේ සංඛ්යා මගිනි. | ||
| − | |||
| − | |||
| − | + | "න මානෙන විනා යුක්තිර් | |
| − | + | ද්රව්යානාං ජායතෙ ක්වවිත්" (මැනුමක් කිරුමක් නැතිව ද්රව්යයන්ගේ ව්යවහාරයෙන් කිසිවිටෙක නොවන්නේ ය.) යනු පැරණි පණ්ඩිත මතයකි. මනුෂ්යාගේ එදිනෙදා කටයුතුවලදී තමන්ට අයිති දේ කොපමණ දැයි බලාගැනීමට මැනුම හා කිරුම අවශ්ය මය. කිරුමෙන් හා මැනුමෙන් ලැබෙන ප්රතිඵලය සටහන් කර තැබීම ද වැදගත් ය. ඒ නිසා හරකකු හෝ බැටළුවකු අයිති මිනිසා තමාට අයිති හරකුන් හෝ බැටළුවන් ගණන හැඳින්වීමට එක යන වචනය යොදා ගත්තේ ය. තව එකෙක් සිටි නම් දෙක යන වචනය ද, මෙසේ එක එකා වැඩිවන විට තු , හතර, පහ ආදි වචන ද යොදා ගැනීමට සිදුවිය. ඒ ඒ රටවල මිනිසුන් එක, දෙක, තුන, ආදි වචන වෙනුවට අනුරූප වචන යොදා ගෙන තිබේ. | |
| − | + | ද්රව්ය සමුහයක තිබෙන ද්රව්ය ගණන කීයදැයි සෙවීම ගණන් කිරීම නම් වේ. ගණන් කිරීමෙන් ලැබෙන සංඛ්යාවලට පුර්ණ සංඛ්යා, ප්රකෘති සංඛ්යා යන නම් දී තිබේ. වඩාත් නිවැරදි ලෙස ගණිත භාෂාවෙන් කියතොත් මේ සංඛ්යා ධනපූර්ණ සංඛ්යා නම් වේ. | |
| − | |||
| − | |||
| − | |||
| − | + | සංඛ්යා භාවිත කිරීමේ දී ප්රධාන ගණිත කර්ම සතරක් තිබේ. එනම් එකතු කිරීම, අඩු කිරීම, ගුණ කිරීම, බෙදීම යනුයි. | |
| + | |||
| + | |||
| + | == එකතු කිරීම සහ අඩු කිරීම: == | ||
| + | එක් ද්රව්ය සමුහයක ද්රව්ය අටක් ද, වෙනත් ද්රව්ය සමූහයක ද්රව්ය පහක් ද තිබේ නම් මුළු ද්රව්ය ගණන 13 ක් වේ. 8 ටෙන් 5 හෙන් මුළු ගණන 13 වේ. සංඛ්යා දෙකක හෝ වැඩි ගණනක මුළු ගණනට ඓක්යය හෝ එකතුව යයි කියනු ලැබේ. මෙහි දී පාව්චිචි කරන ගණිත කර්මය එකතු කිරීම වේ. "+" ලකුණ එකතු කිරීමේ ලකුණය. මෙහි නම ධන යනුයි. | ||
| + | |||
| + | 8 + 5 = 13ය; මෙය කියවන්නේ, අට ධන පහ සමානයි දහතුන කියාය. | ||
බඩු ගොඩවල් දෙකක තිබෙන මුත් මුළු බඩු ගණන සෙවීමේ දී පළමු ගොඩෙන් පටන්ගෙන ගණන් කළත්, දෙවෙනි ගොඩෙන් පටන් ගෙන ගණන් කළත් ලැබෙනක ප්රතිඵලය සමාන බව පැහැදිලිය. | බඩු ගොඩවල් දෙකක තිබෙන මුත් මුළු බඩු ගණන සෙවීමේ දී පළමු ගොඩෙන් පටන්ගෙන ගණන් කළත්, දෙවෙනි ගොඩෙන් පටන් ගෙන ගණන් කළත් ලැබෙනක ප්රතිඵලය සමාන බව පැහැදිලිය. | ||
| − | + | 8 + 5 = 13; 5 + 8 = 13 | |
සංඛ්යා එකතු කිරීමේ ගණිත කර්මයේ දී එක ම අනුපිළිවෙළකට සංඛ්යා ලිවීම අවශ්ය නොවේ. එම නිසා පහත සඳහන් මූලික න්යාය දෙක එකතු කිරීමේ ගණිත කර්මයට බලපායි. | සංඛ්යා එකතු කිරීමේ ගණිත කර්මයේ දී එක ම අනුපිළිවෙළකට සංඛ්යා ලිවීම අවශ්ය නොවේ. එම නිසා පහත සඳහන් මූලික න්යාය දෙක එකතු කිරීමේ ගණිත කර්මයට බලපායි. | ||
| − | 01) | + | '''01) එකතු කිරීමේ පරිවර්තන න්යාය:''' |
| − | + | ||
| − | 02) එකතු කිරීමේ සංඝටන න්යාය : | + | a + b = b + a |
| − | + | ||
| + | '''02) එකතු කිරීමේ සංඝටන න්යාය:''' | ||
| − | + | a + (b + c) = (a + b) + c | |
| − | + | මෙහි a, b, c යන සංකේතවලින් සංඛ්යා හඳුන්වනු ලැබේ. | |
| − | " - | + | 13න් 8ක් අඩු කළ විට 5ක් ද, එසේ ම 13න් 5ක් අඩු කළ විට 8ක් ද ඉතිරි වේ. මේ ගණිත කර්මය අඩුකිරීම වේ. |
| + | |||
| + | "-" ලකුණ අඩු කිරීමේ ලකුණයි. මෙහි නම සෘණ යනුයි. | ||
එක සංඛ්යාවකින් තවත් සංඛ්යාවක් අඩු කළ විට ලැබෙන සංඛ්යාවට අන්තරය යයි කියනු ලැබේ. මෙකී සිද්ධි මෙසේ පෙන්විය හැක; | එක සංඛ්යාවකින් තවත් සංඛ්යාවක් අඩු කළ විට ලැබෙන සංඛ්යාවට අන්තරය යයි කියනු ලැබේ. මෙකී සිද්ධි මෙසේ පෙන්විය හැක; | ||
| − | + | 8 + 5 = 13 | |
| − | |||
| − | |||
| − | |||
| − | 8 | + | 5 + 8 = 13 |
| − | + | 13 - 5 = 8 | |
| − | |||
| − | |||
| − | |||
| − | + | 13 - 8 = 5 | |
| − | + | 8, 5, 13 යන සංඛ්යා තුන වෙනුවට a, b, c සංකේත පාව්ච්චි කර මෙම සිද්ධි පොදු වශයෙන් මෙසේ පෙන්විය හැකිය. a සහ b එකතු කළ විට ඓක්යය c ය. | |
| − | ගුණ කිරීම : එක ම සංඛ්යාව කීපවාරයක් ගෙන එකතු කිරිමෙන් ඓක්යය ලබාගැනීම වෙනුවට එය ලබාගැනීමේ විශේෂ ක්රමයක් ඇත. 7 + 7+ 7 + 7 යන්න කෙටිකර මෙසේ ලිවිය හැක : 7 x 4 මේ ගණිත කර්මයට ගුණකිරීම යයි කියනු ලැබේ. මෙහි | + | a + b = c |
| − | + | ||
| − | පේළියටකට ගඩොල් කැට | + | b + a = c |
| + | |||
| + | c – a = b | ||
| + | |||
| + | c – b = a | ||
| + | |||
| + | අඩු කිරීම එකතු කිරිම් මගින් ද දැක්විය හැක. 13න් 5ක් අඩු කිරීම 5ට කීයක් එකතු කළ විට 13ක් ලැබේ ද යන ප්රශ්නය මතය. | ||
| + | |||
| + | එක දොඩම් ගෙඩියක් තිබෙන තැනට තව දොඩම් ගෙඩියක් දැමූ විට ඒ ගොඩේ දොඩම් ගෙඩි දෙකක් වේ. 1ට 1ක් එකතු කළ විට 2 ලැබේ. මෙසේ 2ට තව එකක් එකතු කිරීමෙන් 3 ද, 3ට තව එකක් එකතු කිරීමෙන් 4 ද ආදි වශයෙන් ලැබෙන නිසා, ගණන් කිරීම එකතු කිරීමක් බව පැහැදිලි වේ. | ||
| + | |||
| + | |||
| + | == ගුණ කිරීම: == | ||
| + | එක ම සංඛ්යාව කීපවාරයක් ගෙන එකතු කිරිමෙන් ඓක්යය ලබාගැනීම වෙනුවට එය ලබාගැනීමේ විශේෂ ක්රමයක් ඇත. 7 + 7+ 7 + 7 යන්න කෙටිකර මෙසේ ලිවිය හැක: 7 x 4 මේ ගණිත කර්මයට ගුණකිරීම යයි කියනු ලැබේ. මෙහි 7ට ගුණ්යය යයි ද එකතු කිරීමට තිබෙන සංඛ්යාවේ වාර ගණන පෙන්වන 4ට ගුණකයයි ද, ගුණ කිරීමෙන් ලැබෙන ප්රතිඵලයට ගුණිතයයි ද කියනු ලැබේ. ලකුණ "X" ගුණ කිරීමේ ලකුණයි. එක කියවන්නේ වරක් කියායි. දෙවරක්, තුන්වරක් ආදි ගුණකිරීමේ වක්ර ගුණිතය සෙවීමට පිහිට වේ. | ||
| + | [[ගොනුව:c-16.jpg|400px|left]] | ||
| + | පේළියටකට ගඩොල් කැට 7ක් බැගින් තිබෙන සේ තිරස් පේළි 4ක් මෙසේ පිළියෙල කළ හැකිය. එවිට සිරස් පේළියක ගඩොල් කැට සතරක් තිබේ. මෙහි ගඩොල් කැට 7 බැගින් තිබෙන තිරස් පේළි 4ක් ද එසේ ම ගඩොල් කැට 4 බැගින් තිබෙන සිරස් පේළි 7ක් ද තිබේ. මුළු ගඩොල් ගණන 7 x 4 ට ද 4 x 7ට ද සමාන වේ. එම නිසා 7 x 4 = 4 x 7 ගුණ කිරීමක දී ගුණ්යය ද ගුණකය ද එක ම අනුපිළිවෙලකට ලිවීම අනවශ්යය. ගුණ කිරීමේ දී මේ වැදගත් තුන්වැනි ගණිත න්යාය බලපාන බව පැහැදිලිය. | ||
| − | (3) ගුණකිරීමේ පරිවර්තනය න්යාය : a x b = b x a 7 x 4 = 28 මෙහි ගුණ්යය වූ | + | '''(3) ගුණකිරීමේ පරිවර්තනය න්යාය:''' a x b = b x a 7 x 4 = 28 මෙහි ගුණ්යය වූ 7ට ද ගුණකය වූ 4ට ද 28 ටේ සාධක යයි කියනු ලැබේ. සාධක තිබෙන නිසා 28 සාධක සංඛ්යාවක් යයි කියනු ලැබේ. |
| − | ඉහත පෙන්වන ලද ගඩොල් තිරස් පේළි | + | ඉහත පෙන්වන ලද ගඩොල් තිරස් පේළි 4රේ තිබෙන එක එක ගඩොල් කැටය උඩ තව ගඩොල් කැටය උඩ තව ගඩොල් කැට 2 බැගින් තබමු. එවිට තිරස් පේළියක තිබෙන ගඩොල් ගණන 3 x 7 වේ. එවැනි පේළි 4ක් තිබෙන නිසා මුළු ගඩොල් ගණන (3 x 7) x 4 ය. එක ගොඩක ඇති ගඩොල් ගණන 3කි. මෙවැනි ගොඩවල් තිරස් පේළියක 7 බැගින් ද සිරස් පේළියක 4 බැගින් ද ඇත. එබැවින් මුළු ගඩොවල් ගණන 7 x 4 වේ. ඒ නිසා මුළු ගඩොල් කැට ගණන 3 x (7 x 4) වේ. (3 x 7) x 4 = 3 x ( 7 x 4). |
| − | අංක ගණිතයේ හතර වැනි වැදගත් න්යාය වූ මෙය පොදු වශයෙන් මෙසේ ලිවිය හැක : | + | අංක ගණිතයේ හතර වැනි වැදගත් න්යාය වූ මෙය පොදු වශයෙන් මෙසේ ලිවිය හැක: |
| − | 04) | + | '''04) ගුණ කිරීමේ සංඝටන න්යාය:''' (a x b) x c = a x (b x c ) |
| − | පළමුවෙන් පිළියෙල කරන ලද ගඩොල් කැට 28 කීප විදියකට දෙකොසකට වෙන් කළ හැකිය. එයින් එකක් ගනිමු. සිරස් පේළි | + | පළමුවෙන් පිළියෙල කරන ලද ගඩොල් කැට 28 කීප විදියකට දෙකොසකට වෙන් කළ හැකිය. එයින් එකක් ගනිමු. සිරස් පේළි 2ක් එක කොටසකට ද 5ක් අනික් කොටසට ද වෙන් කරමු. එවිට පළමුවැනි කොටසේ ගඩොල් කැට 2 x 4ක් ද අනික් කොටසේ 5 x 4ක් ද තිබේ. එහි තිබෙන මුළු ගඩොල් කැට ගණන 2 x 4 + 5 x 4 වේ. එම නිසා 7 x 4 හෙවත් (2 + 5) x 4 = 2 x 4 + 5 x 4. |
මේ පස්වැනි න්යාය ද අංක ගණිතයේ වැදගත් න්යායක් වේ. එය පොදු වශයෙන් මෙසේ ලිවිය හැක: | මේ පස්වැනි න්යාය ද අංක ගණිතයේ වැදගත් න්යායක් වේ. එය පොදු වශයෙන් මෙසේ ලිවිය හැක: | ||
| − | 05) | + | '''05) ගුණ කිරීමේ විඝටනය න්යාය:''' ( a+ b) x c = a x c + b x c |
එකම සංඛ්යාව කිප වරක් ලියා එකතු කිරීම කෙටිකර ගුණ කිරීමක් මෙන් ලියන්නට හැකිවා මෙන් ම, එක ම සංඛ්යාව කීප වරක් ගුණ කිරිමෙන් ලැබෙන අඛණ්ඩ ගුණිතය ද කෙටිකර ලිවීමට ක්රමයක් තිබේ. | එකම සංඛ්යාව කිප වරක් ලියා එකතු කිරීම කෙටිකර ගුණ කිරීමක් මෙන් ලියන්නට හැකිවා මෙන් ම, එක ම සංඛ්යාව කීප වරක් ගුණ කිරිමෙන් ලැබෙන අඛණ්ඩ ගුණිතය ද කෙටිකර ලිවීමට ක්රමයක් තිබේ. | ||
| − | උදා : 6 x 6 x 6 = 63 මෙහි 6 ට උඩින් දකුණු පැත්තෙන් ලියා තිබෙන | + | උදා: 6 x 6 x 6 = 63 මෙහි 6 ට උඩින් දකුණු පැත්තෙන් ලියා තිබෙන 3ට දර්ශකය යි කියනු ලැබේ. මෙහි ගුණිතය 6 යේ 3 වෙනි බලය වේ. දර්ශකය ගුණිතයේ බලයේ තිබෙන සාධක ගණන පෙන්වයි. දර්ශක වාදයෙහි අංක ගණිතයට අවශ්ය වූ වැදගත් න්යාය 4ක් තිබේ. a, b, m, n යන සංඛ්යා සතර ධනපුර්ණ සංඛ්යා වේ නම්, මේ න්යාය සතර මෙසේ ලවිය හැකිය: |
| + | |||
| + | am x an = am+n උදා . 63 x 62 = 65 | ||
| + | |||
| + | (am) n = am n උදා . (52) 3 = 56 | ||
| + | |||
| + | (a x b)m = a x bm | ||
| + | |||
| + | උදා . (3 x 4)2 = 32 x 42 | ||
| + | |||
| + | m යන සංඛ්යාව n යන සංඛ්යාවට වඩා ලොකු නම් am ÷ an = an = am –n | ||
| + | |||
| + | උදා. 75 ÷ 72 = 73 | ||
| + | |||
| − | + | == බෙදීම: == | |
| − | + | 7 x 4 = 28; 28, 4න් බෙදු විට 7 ලැබේ. මෙය ලියන්නේ මෙසේය: 28 ÷ 4 = 7 "÷" බෙදීමේ ලකුණය. මෙහි 28ට භාජ්යය යයි ද 4ට භාජකය යයි ද 7ට ලබ්ධිය යයි ද කියනු ලැබේ. 28ට වනාහි 7හි සහ 4හි ද ගුණාකාරයකි. 28 ÷ 4 යන්නෙහි තේරුම 28 කින් 4 ගොඩවල් කී වරක් අඩු කළ හැකිද? මෙය ගුණ කිරීමේ ප්රතිවිරුද්ධ අදහසය. 7 x 4 යන්නෙහි තේරුම 7 ඒවා 4ක් එකතු කළ විට කීයක් ලැබේ ද යන්නය. | |
| − | |||
| − | + | පොදු වශයෙන් a x b = c නම් c ÷ a = b; c ÷ b = a; c යනු a හි ද b ද ගුණාකාර වේ. | |
| − | + | a සහ b සංඛ්යා දෙකක් වේ නම් a, bට වඩා කුඩා විය හැකිය; නැතහොත් a, bට සමාන විය හැකිය; එසේත් නැතහොත් a, bට වඩා ලොකු විය හැකිය. මෙය සංකේත මගින් ප්රකාශ කරන්නේ මෙසේය. | |
| − | + | a < b a , b ට වඩා කුඩාය. | |
| − | a | + | a = b a , b ට සමානය. |
| − | + | a > b a , b ට වඩා ලොකුය. | |
| − | |||
| − | |||
a > b නම්, b වලින් a බෙදු විට ලබ්ධියක් ද ශේෂයක් ද ලැබේ. | a > b නම්, b වලින් a බෙදු විට ලබ්ධියක් ද ශේෂයක් ද ලැබේ. | ||
| − | + | උදා:- 57 ÷ 6 ; ලබ්ධිය 9 වේ. ශේෂය 3 ය. | |
| − | + | ||
| + | 57 = 6 x 9 + 3 | ||
| − | හැම සංඛ්යාවක් ම ඊට කුඩා සංඛ්යාවකින් බෙදු විට මේ අන්දමට ලබ්ධිය වූ ද, ශේෂය වූ ද පූර්ණ සංඛ්යා දෙකක් ලබාගත හැක. ශේෂය බින්දුව ( 0 ) නම් ලොකු සංඛ්යාවෙන් බෙදිය හැකි යයි කියනු ලැබේ. | + | හැම සංඛ්යාවක් ම ඊට කුඩා සංඛ්යාවකින් බෙදු විට මේ අන්දමට ලබ්ධිය වූ ද, ශේෂය වූ ද පූර්ණ සංඛ්යා දෙකක් ලබාගත හැක. ශේෂය බින්දුව (0) නම් ලොකු සංඛ්යාවෙන් බෙදිය හැකි යයි කියනු ලැබේ. |
| − | 1, | + | 1, 1න් ගුණ කළවිට ගුණිතය 1 ය. 1, 1න් බෙදුවිට ලබ්ධිය 1 ය. 1 සියලු ම පූර්ණ සංඛ්යා වන්ගේ සාධකයෙකි. සංඛ්යාවක් 0න් ගුණ කළ විට ගුණිතය 0 වේ. බින්දුව බින්දුවෙන් බෙදීම නිරර්ථකය. හැම සංඛ්යාවක් ම 1න් ද එම සංඛ්යාවෙන් ම ද බෙදිය හැක. 1 x 3 = 3; 1 x a = a සංඛ්යාවකට 1ත් එම සංඛ්යාවත් හැර වෙන සාධක නැති නම් ඊට මූලසංඛ්යා යයි කියනු ලැබේ. සාමාන්යෙයන් 1 මුලසංඛ්යා යයි කියනු ලැබේ. සාමාන්යයෙන් 1 මූලසංඛ්යාවක් හැටියට සලකන්නේ නැත. නමුත් සමහර විට එය ද මූලසංඛ්යා ගණයට අයත් කොට ගනු ලැබේ. 2, 3, 5, 6, 7, 11, 13 ආදිය මූල සංඛ්යාවෝයි. |
සංඛ්යා වාදය අංක ගණිතයේ උසස් ම කොටසකි. මුලසංඛ්යා ගැන සංඛ්යාවාදයේ ප්රමේයයන් කීපයක් තිබේ. එයින් එකක් නම් සැම සාධක සංඛ්යාවක් ම මූලසංඛ්යාවල ගණිතයක් සේ ප්රකාශ කළ හැකිය යනුයි. සාධකවල පිළිවෙල නොසලකනවා නම් මෙය කළ හැක්කේ එක ම ආකාරයෙනි. | සංඛ්යා වාදය අංක ගණිතයේ උසස් ම කොටසකි. මුලසංඛ්යා ගැන සංඛ්යාවාදයේ ප්රමේයයන් කීපයක් තිබේ. එයින් එකක් නම් සැම සාධක සංඛ්යාවක් ම මූලසංඛ්යාවල ගණිතයක් සේ ප්රකාශ කළ හැකිය යනුයි. සාධකවල පිළිවෙල නොසලකනවා නම් මෙය කළ හැක්කේ එක ම ආකාරයෙනි. | ||
| − | + | උදා: 36 = 4 x 9 = 22 x 32 | |
සාධක සංඛ්යා දෙකක් හෝ ඊට වැඩි ගණනක් ගනිමු. මේ සංඛ්යා සියල්ල ම බෙදිය හැකි ලොකු ම සාධකයක් තිබේ. | සාධක සංඛ්යා දෙකක් හෝ ඊට වැඩි ගණනක් ගනිමු. මේ සංඛ්යා සියල්ල ම බෙදිය හැකි ලොකු ම සාධකයක් තිබේ. | ||
| − | + | උදා: 28 = 22 x 7 | |
| − | + | ||
| + | 42 = 2 x 3 x 7 | ||
| + | |||
| + | 2 ද 7 ද , 28ටේත්, 42කේත් පොදු සාධක වේ. 14 මේ සංඛ්යා දෙකේ ලොකු ම පොදු සාධකයයි. සංඛ්යා ගණනක ලොකු ම පොදු සාධකයට මහා සාධකයයි කියනු ලැබේ. | ||
| − | + | එසේ ම සංඛ්යා කීපයකින් බෙදිය හැකි ඒ සංඛ්යාවල කුඩා ම ගුණාකාරයන් තිබේ. එයට කුඩා ම පොදු ගුණාකරයයි කියනු ලැබේ. 28ටේන් 42කේත් කුඩා ම පොදුගුණාකාරය 22 x 3 x 7 එනම් 84 වේ. | |
| − | + | a යනු bට වඩා ලොකු සංඛ්යාවක් නම් a = b x q + r මෙහි q ලබ්ධිය වේ. r ශේෂය වේ. bට වඩා r කුඩාය. a සහ bහි පොදු සාධකයක් වේ. මෙසේ a සහ b යන සංඛ්යා දෙකේ මහා පොදු සාධකය b සහ r යන සංඛ්යා දෙකේ මහාපොළ සාධකයට සමානය. ශේෂය වූ r යන්නෙන් b බෙදීමෙන් මෙය ලැබේ. | |
| − | + | b = r x p + s | |
| − | + | දැන් b සහ rහි මහාපොදු සාධකය r සහ sහි මහාපොදු සාධකයට සමානය. මෙසේ ශේෂයෙක් නැතිවන තුරු ශේෂයෙන් භාජකය බෙදීමෙන් සංඛ්යා දෙකක මහාපොදු සාධකය සෙවිය හැකි මේ ක්රියාවලියෙහි දී ලැබෙන අවසාන පූර්ව ශේෂය සංඛ්යා ද්වයේ මහාපොදු සාධකයයි. | |
| − | |||
| − | භාග : a ÷ | + | == භාග: == |
| + | a ÷ bයන් බෙදීමකි. එය මෙසේ ද ලිවිය හැක: මෙය කියවන්නේ aයට b කියාය. මේ ආකාරයට ලියන ලද බෙදීමට හැටියට සලකන විට භාජ්යය වූ aට, භාගයක් හැටියට සලකන විට ලවයයි කියනු ලැබේ. භාජකය වූ bට හරයයි කියනු ලැබේ. a ÷ b බෙදීමෙන් ලැබෙන සම්පූර්ණ ලබ්ධිය යන භාගයෙන් හැඳින්වේ. | ||
| − | උදා . | + | උදා. = 4; හි සම්පූර්ණ ලබ්ධිය 4 වේ. නමුත් 25 ÷ 7හි ලබ්ධිය 3 වේ. 4 වූ ශේෂයක් ලැබේ. |
| − | ඉහත පෙන්වූ ආකාරයෙන් 25 ÷ 7 යන බෙදීමේ සම්පූර්ණ ලබ්ධිය | + | ඉහත පෙන්වූ ආකාරයෙන් 25 ÷ 7 යන බෙදීමේ සම්පූර්ණ ලබ්ධිය මෙන් පෙන්විය හැකිය. |
| − | + | =; මේ බෙදීමේ සම්පූර්ණ ලබ්ධිය වේ. මෙය ලියන්නේ මෙනි. | |
| − | භාගය කියන්නේ සංඛ්යාවකින් කොටසකටය. යමක් සමාන කොටස් දෙකකට බෙදු විට ලැබෙන කොටසට හෙවත් භාගයට එයින් බාගයයි කියනු ලැබේ. 1 , 2 බෙදු විට ලැබෙන්නේ බාගයයි. එනම් යි. | + | භාගය කියන්නේ සංඛ්යාවකින් කොටසකටය. යමක් සමාන කොටස් දෙකකට බෙදු විට ලැබෙන කොටසට හෙවත් භාගයට එයින් බාගයයි කියනු ලැබේ. 1, 2 බෙදු විට ලැබෙන්නේ බාගයයි. එනම් යි. |
| − | මැනිමේ සහ කිරීමේ දී සියලු දේ ම ඒකක සම්පූර්ණ ගණනකින් මැනිය හෝ කිරිය නොහැකිය. බාල්කයක දිග අඩිවලින් මනින විට එහි තිබෙන අඩි ගණන සංඛ්යාවකින් පමණක් | + | මැනිමේ සහ කිරීමේ දී සියලු දේ ම ඒකක සම්පූර්ණ ගණනකින් මැනිය හෝ කිරිය නොහැකිය. බාල්කයක දිග අඩිවලින් මනින විට එහි තිබෙන අඩි ගණන සංඛ්යාවකින් පමණක් සම්පූර්ණයෙන් මැනීමට නොහැකිවන්නට පුළුවන. |
| − | බාල්කයක දිගෙහි සම්පූර්ණ අඩි 12ක් ද අඩියකට අඩු කොටසක් ද තිබිය හැකිය. බර කිරීමේ දී ද එසේ මය. අඩියට අඩු කොටස මැනීමට අඩිය සමාන කොටස් 12කට බෙදා එක කොටසකට අඟල යයි කියනු ලැබේ. | + | බාල්කයක දිගෙහි සම්පූර්ණ අඩි 12ක් ද අඩියකට අඩු කොටසක් ද තිබිය හැකිය. බර කිරීමේ දී ද එසේ මය. අඩියට අඩු කොටස මැනීමට අඩිය සමාන කොටස් 12කට බෙදා එක කොටසකට අඟල යයි කියනු ලැබේ. එසේම බර කිරීමේ දී රාත්තලට අඩු කොටස මැනීමට අවුන්ස යයි කියන සමාන කොටස් 16කට රාත්තල බෙදා තිබේ. |
| − | බාල්කයක දිග අඩි 8 අඟල් 5 කියනවා වෙනුවට එහි දිග අඩි | + | බාල්කයක දිග අඩි 8 අඟල් 5 කියනවා වෙනුවට එහි දිග අඩි කියා දැක්විය හැකිය. අඟලක් අඩියකින් දොළහෙන් පංගුවය.; අඟල් 1 = අඩි අඟල් 5 එවැනි කොටස් 5; අඟල් 5 = අඩි |
භාගයක ලවය හරයට අඩු නම් ඊට නියම භාග යයි ද අනික් භාගවලට විෂම භාග යයි ද කියනු ලැබේ. භාගවල හරය සම නම් භාග එකතු කිරීම ද අඩු කිරීම ද පහසුය. | භාගයක ලවය හරයට අඩු නම් ඊට නියම භාග යයි ද අනික් භාගවලට විෂම භාග යයි ද කියනු ලැබේ. භාගවල හරය සම නම් භාග එකතු කිරීම ද අඩු කිරීම ද පහසුය. | ||
| − | උදා . | + | උදා. න් පංගු තුනක් ද පංගු දෙකක් ද එකතු කළ විට 7න් පංගු 5ක් ලැබේ. |
| − | + | න් කොටසක් 4කින් එවැනි කොටස් 2ක් අඩු කළ විට 7න් කොටස් 2ක් ලැබේ. | |
| − | + | යන භාගයේ හරයට හා ලවයට ද පොදු සාධක නැත. එවැනි භාග කුඩා ම ස්වරූපයෙන් ලියා තිබේ. භාගයක ලවය ද හරය ද එක ම සංඛ්යාවෙන් ගුණ කිරිමෙන් හෝ බෙදීමෙන් භාගයේ වටිනාකම වෙනස් නොවේ. | |
| − | උදා . | + | උදා. ; මෙහි හරය ද ලවය ද 2න් ගුණ කර තිබේ. |
| − | + | ; මෙහි හරය ද ලවය ද 3න් බෙදා තිබේ. | |
| − | + | ; අඟල් 4ක් 6ට බෙදුවත් අඟල් 2ක් තුනට බෙදුවත් ලැබෙන දිග ප්රමාණය සමානය. භාගවල හර වෙනස් වූ විට ඒවා සමාන හරයක් සහිත භාගයකට පෙරලීමෙන් ඒ සියලු ම භාග එකතු කිරීම ද අඩු කිරීම ද කළ හැක. | |
| − | උදා . | + | උදා. |
භාග දෙකක් ගුණ කරන්නේ මෙසේය. | භාග දෙකක් ගුණ කරන්නේ මෙසේය. | ||
| − | + | න් ගුණ කිරීම වෙනුවට 2න් ගුණ කළහොත් ලැබෙන ගුණිතය 5 ගුණයක් ලොකුය. මන්ද? , 2න් පහෙන් පංගුව නිසාය. එම නිසා න් ගුණ කිරීමට 2න් ගුණ කර ලැබෙන ගුණිතය 5න් බෙදිය යුතුය. | |
| − | + | න් නේ පරස්පරය යයි කියනු ලැබේ. භාගයක පරස්පරයක් ලබාගැනීමට ලවය හරය කර හරය ලවය කර භාගය ලිවිය යුතුය. භාගයක් භාග යෙකින් බෙදීමට පරස්පරයෙන් ගුණ කළ යුතුය. | |
| − | + | න් බෙදනවා වෙනුවට එය 2න් බෙදුවොත් භාජකය 5 ගුණයක් අඩු වන නිසා 2න් බෙදු විට ලැබෙන ලබ්ධිය 5න් ගුණ කළ යුතුය. | |
| − | + | ||
| + | එම නිසා | ||
| − | |||
| − | |||
| − | + | == දශම භාග: == | |
| + | 1ට අඩු සංඛ්යා නියම භාග මෙන් පමණක් නොව තවත් ක්රමයකට ද ලිවිය හැක. එනම්, පූර්ණ සංඛ්යාවන් පිළිබඳ ස්ථානීය අගය සුත්රයේ අනුසාරයෙන් දශම ක්රමයෙන් ප්රකාශ කළ හැකිය. අඩියකට අඩු කෑල්ලක් ඉතිරි වේ නම්, එය අඟල්වලින් මනිනවා වෙනුවට අඩිය සම කොටස් 10කට බෙදා එවැනි කොටස් කීයකට එහි දිග සමාන දැයි සෙවිය හැකිය. අඩි ගණන 17යි කියා ගනිමු. අඩියට අඩු කෑල්ලේ අඩියෙන් 10න් පංගු 3ක් තිබුණ හැටියට ගනිමු. අඩියෙන් 10න් පංගුවකට අඩු තවත් කෑල්ලක් තිබේ නම් අඩියෙකන් සම කොටස් 100කට බෙදා එවැනි කොටස් කීයක් ඉතිරි කොටසේ තිබේ දැයි සෙවිය හැකිය. එවැනි කොටස් 7ක් තිබුණි නම් බාල්කයේ දිග අඩි යි. තවත් කොටසක් ඉතිරි වේ නම් කොටසක් සම කොටස් 10කට බෙදා එනම් | ||
| + | අඩියෙන් 1000න් පංගු ගෙන එහි එවැනි කොටස් කීයක් තිබේ දැයි සෙවිය හැකිය. මෙසේ ආදි කොටස්වලට අඩිය බෙදීමෙන් බාල්කයේ දිග දශම ක්රමයෙන් ප්රකාශ කළ හැකිය. | ||
| − | + | මේ දශම ක්රමය පුර්ණ සංඛ්යා ලියන ක්රමය පුළුල් කිරීමකි. 3857 දශම ක්රමයට ලියන ලද සංඛ්යාවක් නම් එහි වටිනාකම මේ අන්දමට ලිවිය හැකිය. 3857 = 3 x 103 + 8 x 102 + 5 x 10 +7 | |
| − | + | දැන් මේ සංඛ්යාවේ 1000 ඒවා වෙන්කර ඊට පසු 100 ඒවා වෙන්කර ඊට පසුව 10 ඒවා වෙන්කර ඊට පසුව 1 ඒවා ලබාගෙන තිබේ. දැන් 1ට අඩු කොටසක් තිබේ නම් එහි ඒවා වෙන්කර ඉතිරි කොටසේ ඒවා වෙන්කර එසේම ඒවා ඒවා ආදි වශයෙන් වෙන්කර සංඛ්යාවේ වටිනාකම ලිවිය හැකිය. | |
| − | + | යන සංඛ්යාව මෙසේ ප්රකාශ කරන විට හි ඒවා කොපමණ තිබේ දැයි සෙවිය යුතුය. හි ඒවා ක් හෙවත් ඒවා 1ක් ද ඒවායින් ක්ද තිබේ. ඒවා හි ඒවා හෙවත් තිබේ. ඒවා හි ඒවා 5ක් තිබේ. එම නිසා මෙය සථානීය අගය යන සුත්රය අනුව මෙසේ ලියනු ලැබේ: = 14.125 මෙහි 4ටත් 1ටත් අතර තිබෙන තිතට දශම තිත යයි කියනු ලැබේ. එය ලියන්නේ මැදට ටිකක් උඩින්ය. එයින් එකේ ඒවා ගණන ඒවා ගණනින් වෙන්කර දැක්වේ. | |
පූර්ණ සංඛ්යාව ද දශම භාග ද ස්ථානීය අගය සුත්රය අනුව ලියන ලද සංඛ්යා නිසා, මේ සංඛ්යා එකතු කරන්නේ ද අඩු කරන්නේ ද එක ම ක්රම යෙනි. එනම්, ස්ථානීය අගය සම වූ සංඛ්යා එක යට එක ලිවීමෙනි. | පූර්ණ සංඛ්යාව ද දශම භාග ද ස්ථානීය අගය සුත්රය අනුව ලියන ලද සංඛ්යා නිසා, මේ සංඛ්යා එකතු කරන්නේ ද අඩු කරන්නේ ද එක ම ක්රම යෙනි. එනම්, ස්ථානීය අගය සම වූ සංඛ්යා එක යට එක ලිවීමෙනි. | ||
| − | + | පුර්ණ සංඛ්යාවකින් ගුණ කරන්නේ ගුණ කිරීමේ චක්ර මගින් බව කලින් කියා ඇත. සංඛ්යාවක් 357 වැනි ලොකු සංඛ්යාවකින් ගුණ කරන විට පළමුව 300න් ද දෙවනුව 50න් ද තුන්වෙනුව 7න් ද ගුණකර ලැබෙන ගුණිතයන් එකතු කර සම්පූර්ණ ගුණිතය ලබාගත හැකිය. | |
| − | + | දශම භාග ගුණකිරීමේ දී දශම තිත නොසලකා පූර්ණ සංඛ්යා මෙන් ගුණකර ගුණිතයේ දශමස්ථාන ගණන ගුණයේ ද ගුණකයේ ද තිබෙන දශමස්ථාන ගණන්වල ඓක්යයට සමාන වන සේ දශම තිත තැබීමෙන් නිවැරදි ගුණිතය ලබාගත හැකිය. | |
| − | |||
| − | + | == සංඛ්යාවකින් බෙදීම: == | |
| − | + | 10න් හෝ 10ට අඩු සංඛ්යාවකින් බෙදන විට එය කෙටි ක්රමයෙන් කළ හැකිය. 9න් 6745 බෙදීම යනු 9 ඒවා කීයක් එකතු කළ විට 6745 ලැබේ ද නැතහොත් 6745න් 9 ඒවා කීයක් අඩුකළ හැකි ද යන්න සෙවීමයි. 6745හි තිබෙන්නේ 1000 ඒවා 6කි. එම නිසා 6745හි තිබෙන 9 ඒවා ගණන 1000ට අඩුය. 6745හි 100 ඒවා 67ක් තිබේ. 67, 9 බෙදීමෙන් 6745න් 9 ඒවා 700ක් අඩු කළ හැකි බව පෙනේ. ඉතිරි වන්නේ 445යි. 445ට දහයේ ඒවා 44කි. 9න් 44 බෙදීමෙන් 445න් 9 ඒවා 40ක් අඩු කළ හැකි බව පෙනේ. ඊට පසු ඉතිරිවන 85න් 9 ඒවා 9ක් කළ විට 4ක් ඉතිරි වන බව පෙනේ. එම නිසා 6745න් 9 ඒවා 749ක් අඩුකළ හැකිය. 4ක් ඉතිරි වේ. මෙම බෙදීම ලියන්නේ මෙසේය. | |
| − | + | 9 6745 හෝ 6745 = 749 | |
| + | |||
| + | 749 - 4 9 | ||
| − | + | 10ට වඩා ලොකු සංඛ්යාවකින් බෙදීම කරන්නේ ද මේ අන්දමටය. | |
| + | |||
| + | 45237 , 57න් බෙදීමේ දී භාජ්යයේ තිබෙන 10,000 ඒවා ගණන වත් 1000 ඒවා ගණන වත් 57න් බෙදිය නොහැකි බව පෙනේ. එම නිසා පළමුව 100 ඒවා ගණන වූ 452 ගෙන එහි 57 ඒවා කීයක් තිබේ දැයි බැලිය යුතුයි. ඒ ගණන 100 ඒවායෙන් අඩුකර ඉතිරි ගණන 57න් බෙදිය යුතුයි. | ||
මේ බෙදීම කරන්නේ මෙසේයි. | මේ බෙදීම කරන්නේ මෙසේයි. | ||
| − | + | 793 100 ඒවා 452න් 57 ඒවා 7ක් අඩු කළ හැකිය. ඉතිරි වන්නේ 10 ඒවා 533 කි. එයින් 57 ඒවා | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 57 45239 9ක් අඩු කළ හැකිය. එම නිසා ලබ්ධියේ දශස්ථානයට 9 ලැබේ. දැන් ඉතිරි වන්නේ 209යි. | |
| + | |||
| + | 399 මෙයින් 57 ඒවා 3ක් අඩු කළ විට 38ක් ඉතිරි වේ. | ||
| − | 3.57 100 ගුණ කළ විට | + | 533 |
| + | |||
| + | 513 | ||
| + | |||
| + | 209 | ||
| + | |||
| + | 171 | ||
| + | |||
| + | 38 | ||
| + | |||
| + | දශම භාග බෙදීමේ දී භාජකය පුර්ණ සංඛ්යාවක් කර මේ අන්දමට ම බෙදීම කළ හැකිය. දශම භාගයක් පූර්ණ සංඛ්යාවක් කරනුයේ 10න් හෝ 100න් හෝ 1000න් හෝ 10යේ අන්කිසි බලයකින් ගුණ කිරීමෙනි. 10යේ බලය භාගයේ දශමස්ථාන ගණනට සමානය. | ||
| + | |||
| + | 3.57 100 ගුණ කළ විට 357ක් ලැබේ. දශම ස්ථාන ගණන 2 නිසා 100න් හෙවත් 10යේ දෙවැනි බලයෙන් ගුණකළ යුතුයි. භාජකය පූර්ණ සංඛ්යා වක් කිරීමට 10යේ බලයකින් ගුණ කරනවා නම් භාජ්යය ද එම දහයේ බලයෙන් ම ගුණකළ යුතුයි. එම නිසා මේ අන්දමට භාජකය ද භාජ්යය ද වෙනස් කර බෙදීම කළ හැකිය. දශම භාගයකින් බෙදීම තවත් අන්දමකට කළ හැකිය. භාජ්යයේ ද භාජකකයේ ද දශම තිත් නොසලකා බෙදීම කර අවසානයේ දී ලබ්ධියේ දශම තිත තැබීම දළ උත්තරයක් ලබාගැනීමෙන් කළ හැකිය. ([[දශම භාග]] බ.) | ||
සාමාන්ය භාග සියල්ල ම දශම භාග හැටියට ලිවිය හැකිය. ලවය හරයෙන් බෙදීමෙන් භාගයට සමාන දශම භාගය සොයා ගත හැකිය. සමහර විට ලැබෙන දශම භාගයේ එක ම අංක පිළිවෙළට ආවර්ත වෙමින් ලැබෙන බව පෙනෙනවා ඇත. එසේ වන විට බෙදීම නවත්වා ආවර්ත වන අංකවලින් පළමු වැනි අංකයේ ද අනිත්ම අංකයේ ද උඩින් තිත් තැබීමෙන් ඒවා දැක්විය යුතුය. | සාමාන්ය භාග සියල්ල ම දශම භාග හැටියට ලිවිය හැකිය. ලවය හරයෙන් බෙදීමෙන් භාගයට සමාන දශම භාගය සොයා ගත හැකිය. සමහර විට ලැබෙන දශම භාගයේ එක ම අංක පිළිවෙළට ආවර්ත වෙමින් ලැබෙන බව පෙනෙනවා ඇත. එසේ වන විට බෙදීම නවත්වා ආවර්ත වන අංකවලින් පළමු වැනි අංකයේ ද අනිත්ම අංකයේ ද උඩින් තිත් තැබීමෙන් ඒවා දැක්විය යුතුය. | ||
| − | උදා. | + | උදා. දශම භාගයක් කරන විට 027 ආවර්ත වෙමින් ලැබෙන බව පෙනේ. මෙය ලියන්නේ මෙසේය. |
| + | |||
| + | = .027027 = .027 | ||
| + | |||
| + | මෙවැනි දශම භාගවලට ආවර්ත දශම භාගයයි කියනු ලැබේ. ([[ආවර්ත දශමය]] බ.) | ||
| + | |||
| + | |||
| + | == අපරිමේය සංඛ්යා: == | ||
| + | 2 x 2 = 4; 3 x 3 = 9; මෙය සලකා බලමු. 2ට හතරේ වර්ගමූල යැයි යයි කියනු ලැබේ. 3, 9යේ වර්ගමූලය වේ. මෙසේ 4ට ද 9ට වර්ගමූල තිබේ. 4 ද 9 ද වර්ග පූර්ණ සංඛ්යාවකින් ප්රකාශ හැකි නමුත් 2, 3, 5, 7, 8 ආදි සංඛ්යාවක වර්ගමූල පූර්ණ සංඛ්යාවකින්හෝ සාමාන්ය භාගයකින් හෝ දශම භාගයකින් හෝ නිවරදිව ප්රකාශ කළ නොහැකිය. | ||
| + | |||
| + | 2කේ වර්ගමූලය ලියන්නේ මෙසේය: .2කේ වර්ගමූලය ඉතා ආසන්න වශයෙන් සෙවිය හැකිය. දෙකේ වර්ගමූලය 1ටත් 2ටත් අතර සංඛ්යාවක් වන නමුත් එය නිවැරදිව මෙපමණ යැයි කිව නොහැකි බවත් ඍජුකෝණි ත්රිකෝණයක පාද දෙක අඟල් 1 බැගින් දිග නම් එහි කර්ණයේ දිග අඟල් බවත් අවුරුදු 2500කටත් පෙර සිටි පෛතගොරස් නමැති පණ්ඩිතයා පෙන්වා දුන්නේ ය. මේ ත්රිකෝණයේ කර්ණය අඟල් ට සමාන සරල රේඛාවක් වේ. නමුත් එහි දිග කොපමණ දැයි දශම භාගවලින් හෝ සාමාන්ය භාගවලින් නිවැරදිව මැනිය නොහැක. | ||
| − | + | වැනි සංඛ්යාවන්ට අපරිමේය සංඛ්යා යයි කියනු ලැබේ. අපරිමේය සංඛ්යා යනු දශම භාග සාමාන්ය භාගවලින් නිවැරදිව ප්රකාශ කළ නොහැකි සංඛ්යායි. දර්ශකය අනුව අපරිමේය සංඛ්යා ද ගණිත කර්මවලට යෙදිය හැකිය. පළමුවෙන්ම විස්තර කරන ලද දර්ශක නිතිවල දී දර්ශක පූර්ණ සංඛ්යා හැටියට සලකා ඇත. | |
| − | + | නමුත් එම නිතිවල දර්ශක මොනවා වුවත් ඒ නිති සැබෑ බව පිළිගත් විට, සංඛ්යාවක බලයක් මෙන් පෙන්විය හැක. | |
| − | + | 2 කේ වර්ගමූලය 2 කේ n බලය යයි සලකමු. | |
| − | + | 2n x 2n = 2 | |
| − | + | 22n = 2 | |
| − | + | 2n = 21/2 | |
| − | + | ||
| − | + | n = ½ | |
| − | + | ||
| − | + | = 21/2 | |
| − | |||
| − | |||
මේ අන්දමට භාග දර්ශක යොදා අපරිමේය සංඛ්යා වල ලක්ෂණ සෙවිය හැක. | මේ අන්දමට භාග දර්ශක යොදා අපරිමේය සංඛ්යා වල ලක්ෂණ සෙවිය හැක. | ||
| − | පුර්ණ සංඛ්යා යන්නය වඩා නිවැරදි නම ධන පූර්ණ සංඛ්යා බව කලින් කියා ඇත. බින්දුවට අඩු සංඛ්යා තිබිය හැකි බව පැහැදිලි කරුණකි. පූර්ණ සංඛ්යාවකින් 1 බැගින් අඩු කරගෙන යන විට අවසානයේ දී 3, 2, 1, 0 වශයෙන් ලැබේ. බින්දුවට එකක් අඩු සංඛ්යාව 0 – 1 එනම් - 1 | + | පුර්ණ සංඛ්යා යන්නය වඩා නිවැරදි නම ධන පූර්ණ සංඛ්යා බව කලින් කියා ඇත. බින්දුවට අඩු සංඛ්යා තිබිය හැකි බව පැහැදිලි කරුණකි. පූර්ණ සංඛ්යාවකින් 1 බැගින් අඩු කරගෙන යන විට අවසානයේ දී 3, 2, 1, 0 වශයෙන් ලැබේ. බින්දුවට එකක් අඩු සංඛ්යාව 0 – 1 එනම් - 1 වේ. මෙයට සෘණ එක යයි කියනු ලැබේ. ඊට එකක් අඩු සංඛ්යාව - 2 වේ. සෘණ සංඛ්යා මගින් දර්ශක වාදය තවත් පුළුල් කොට ගත හැකිය. |
33 = 27 | 33 = 27 | ||
| + | |||
32 = 9 | 32 = 9 | ||
| − | 31 = 3 | + | |
| − | 30 = 1 | + | 31 = 3 |
| + | මෙහි දෙපැත්තේ ම සංඛ්යාවන් තුනෙන් බෙදීමෙන් | ||
| + | 30 = 1 | ||
| + | දර්ශක වාදය අනුව මේ සත්ය අපට ලැබේ. | ||
3 - 1 = 1/3 | 3 - 1 = 1/3 | ||
| + | |||
3 – 2 = 32 | 3 – 2 = 32 | ||
| − | දර්ශකය 0 නම්, බලයේ වටිනාකම | + | දර්ශකය 0 නම්, බලයේ වටිනාකම 1ය. දැන් දශම භාග සංඛ්යාවකින් මෙසේ ප්රකාශනයක් හැටියට ලිවිය හැකිය:- |
| − | 612.374 = 6 x 102 + 101 + 2 x 100 + 3 x 10-1 + 7 x 10-2 + 4 x 10-3 මෙහි සියලු ම අංක 10 බලයකින් ගුණකර | + | |
| − | ලඝුගණක : ගුණ කිරීමක ද, බෙදීමක ද දශම ස්ථාන ගණනකය නිවැරදි උත්තරයක් දර්ශකවාදයෙහි ප්රතිඵලයක් වන ලඝුගණක මාර්ගයෙන් ලබාගැනීම පහසුය. සංඛ්යාවක් 10 යේ බලයක් හැටියට ප්රකාශ කරන විට, එහි දර්ශකය එම සංඛ්යාවේ ලඝුගණකය වේ. | + | 612.374 = 6 x 102 + 101 + 2 x 100 + 3 x 10-1 + 7 x 10-2 + 4 x 10-3 මෙහි සියලු ම අංක 10 බලයකින් ගුණකර තිබේ. |
| + | |||
| + | |||
| + | == ලඝුගණක: == | ||
| + | ගුණ කිරීමක ද, බෙදීමක ද දශම ස්ථාන ගණනකය නිවැරදි උත්තරයක් දර්ශකවාදයෙහි ප්රතිඵලයක් වන ලඝුගණක මාර්ගයෙන් ලබාගැනීම පහසුය. සංඛ්යාවක් 10 යේ බලයක් හැටියට ප්රකාශ කරන විට, එහි දර්ශකය එම සංඛ්යාවේ ලඝුගණකය වේ. | ||
උදා. 102 = 100. | උදා. 102 = 100. | ||
| − | + | 100යේ ලඝුගණකය (10 පාදයට) = 2 | |
| + | |||
ලඝු 10 100 =2 | ලඝු 10 100 =2 | ||
ලඝුගණක චක්ර මගින් සංඛ්යා දෙකක ලඝුගණකය සොයා ගත් විට සාධක දෙකක් ගුණකිරීම එකතු කිරීමක් වේ. බෙදීම අඩුකිරීමක් වේ. | ලඝුගණක චක්ර මගින් සංඛ්යා දෙකක ලඝුගණකය සොයා ගත් විට සාධක දෙකක් ගුණකිරීම එකතු කිරීමක් වේ. බෙදීම අඩුකිරීමක් වේ. | ||
| − | උදා : ලඝු a = m ; a = 10m | + | උදා: ලඝු a = m ; a = 10m |
| + | |||
ලඝු b = m; b = 10n | ලඝු b = m; b = 10n | ||
| − | |||
| − | + | a x b = 10m x 10m = 10m+n | |
| − | සංඛ්යා : මෙහි විස්තර කර තිබෙන සංඛ්යා සාමාන්ය වශයෙන් පූර්ණ සංඛ්යා, මූල සංඛ්යා සමාන භාග, දශම භාග අපරිමේය සංඛ්යා යන වර්ගවලට ඇතුළත් වේ. මේ සියලු ම සංඛ්යා තාත්වික සංඛ්යා ගණයට අයත් වේ. | + | දැන් m + n ලඝුගණකය වූ සංඛ්යාව චක්රයෙන් සොයාගෙන a x b ගුණිතය ලබාගත හැකිය. (එකතු කිරීමට ද අඩු කිරීමට ද පුදුම යන්ත්ර අද මනුෂ්යයා සොයා ගෙන තිබේ. පැරණි කාලයේ පාව්චිචි කළ ගණිත චතුරස්රය එකතු කිරීමට පාව්චිචි කළ යන්ත්රයකි. සර්පණ රූල අද පාවිච්චි කරන සාමාන්ය උපකරණයකි.) |
| + | |||
| + | |||
| + | == සංඛ්යා: == | ||
| + | මෙහි විස්තර කර තිබෙන සංඛ්යා සාමාන්ය වශයෙන් පූර්ණ සංඛ්යා, මූල සංඛ්යා සමාන භාග, දශම භාග අපරිමේය සංඛ්යා යන වර්ගවලට ඇතුළත් වේ. මේ සියලු ම සංඛ්යා තාත්වික සංඛ්යා ගණයට අයත් වේ. | ||
| + | |||
| + | 1. එකේ වර්ග මුලය වේ. නමුත් - 1කේ වර්ග | ||
| + | |||
| + | මූලය කුමක්ද? එය අපට | ||
| − | |||
| − | |||
මෙසේ ලිවිය හැක; | මෙසේ ලිවිය හැක; | ||
මේ සංඛ්යාව ඒ සංඛ්යාවෙන් ම ගුණ කළ විට -1 ලැබෙන බව අපට කිව හැකිය. නමුත් එහි වටිනාකම සෙවිය නොහැක. අංක ගණිතයේ දි මේ සංඛ්යාව භාවිත කරනු නොලැබේ. එවැනි සංඛ්යාවලට අතාත්වික සංඛ්යා යයි කියනු ලැබේ. මේ අතාත්වික සංඛ්යාවල ප්රයෝජනය කුමක් දැයි ගණිතය නොදන්නා කෙනෙකුට කල්පනා කළ නොහැකිය. නමුත් ගණිතයේ ද විද්යාවේ ද මෙය විශෙෂයෙන් බලපාන සංඛ්යාවකි. | මේ සංඛ්යාව ඒ සංඛ්යාවෙන් ම ගුණ කළ විට -1 ලැබෙන බව අපට කිව හැකිය. නමුත් එහි වටිනාකම සෙවිය නොහැක. අංක ගණිතයේ දි මේ සංඛ්යාව භාවිත කරනු නොලැබේ. එවැනි සංඛ්යාවලට අතාත්වික සංඛ්යා යයි කියනු ලැබේ. මේ අතාත්වික සංඛ්යාවල ප්රයෝජනය කුමක් දැයි ගණිතය නොදන්නා කෙනෙකුට කල්පනා කළ නොහැකිය. නමුත් ගණිතයේ ද විද්යාවේ ද මෙය විශෙෂයෙන් බලපාන සංඛ්යාවකි. | ||
| − | පූර්ණ සංඛ්යා : පූර්ණ සංඛ්යා කීප වර්ගයකට බෙදිය හැක. 1, 2,3,4,5,6,7 ආදි වශයෙන් සීමාවක් නැතිව පූර්ණ සංඛ්යා තිබේ. පූර්ණ සංඛ්යා ගණන අනන්තය. පුර්ණ සංඛ්යාවන් සාධක සංඛ්යා මූල සංඛ්යා යන කොටස් දෙකට බෙදා ඇත. මූල සංඛ්යාවල ගණන ද අනන්තය. මෙය යුක්ලිඩ් විසින් පෙන්වා දෙන ලදි. සංඛ්යා වාදය මූල සංඛ්යාවල ලක්ෂණ පෙන්වා දෙයි. නමුත් සාමාන්ය මනුෂ්යන් දැනගත යුතු පූර්ණ සංඛ්යා වර්ග කිපයක් තිබේ. 1, 3,5,7 ආදි ලැබෙන සංඛ්යාවලට ඔත්තේ යයි කියනු ලැබේ. පළමුවෙනි ඔත්තේ සංඛ්යා දෙක එකතු කළ විට 4 ද තුන එකතු කළ විට 9 ද හතර එකතු කළ විට 16 ද ආදි වශයෙන් ලැබේ. | + | '''පූර්ණ සංඛ්යා:''' පූර්ණ සංඛ්යා කීප වර්ගයකට බෙදිය හැක. 1, 2, 3, 4, 5, 6, 7 ආදි වශයෙන් සීමාවක් නැතිව පූර්ණ සංඛ්යා තිබේ. පූර්ණ සංඛ්යා ගණන අනන්තය. පුර්ණ සංඛ්යාවන් සාධක සංඛ්යා මූල සංඛ්යා යන කොටස් දෙකට බෙදා ඇත. මූල සංඛ්යාවල ගණන ද අනන්තය. මෙය යුක්ලිඩ් විසින් පෙන්වා දෙන ලදි. සංඛ්යා වාදය මූල සංඛ්යාවල ලක්ෂණ පෙන්වා දෙයි. නමුත් සාමාන්ය මනුෂ්යන් දැනගත යුතු පූර්ණ සංඛ්යා වර්ග කිපයක් තිබේ. 1, 3, 5, 7 ආදි ලැබෙන සංඛ්යාවලට ඔත්තේ යයි කියනු ලැබේ. පළමුවෙනි ඔත්තේ සංඛ්යා දෙක එකතු කළ විට 4 ද තුන එකතු කළ විට 9 ද හතර එකතු කළ විට 16 ද ආදි වශයෙන් ලැබේ. |
| − | ඔත්තේ සංඛ්යා | + | '''ඔත්තේ සංඛ්යා:''' 1, 3, 5, 7, 9, 11, 13 |
| − | වර්ග සංඛ්යා : 1, 4, 9, 16, 25, 36, 49 | + | '''වර්ග සංඛ්යා:''' 1, 4, 9, 16, 25, 36, 49 |
| − | මෙසේ | + | මෙසේ 1න් පටන් ගන්නා ඔත්තේ සංඛ්යා ගණනක ඓක්යය එම ගණයේ වර්ගය බව පෙනේ. |
| − | උදා. මුල් ඔත්තේ සංඛ්යා | + | උදා. මුල් ඔත්තේ සංඛ්යා 15හේ ඓක්යය 152 වේ. 2, 4, 6, 8, 10 ආදි 2 බැගින් එකතු කර ලැබෙන සංඛ්යාවලට "ඉරට්ට" හෙවත්ත "ඉරත්ත" සංඛ්යා යයි කියනු ලැබේ. |
ඔත්තේ සංඛ්යා ද ඉරට්ටේ සංඛ්යා ද පූර්ණ සංඛ්යා ද එකට එකක් අනුරූප වන අන්දමට මෙසේ ලියන්න. | ඔත්තේ සංඛ්යා ද ඉරට්ටේ සංඛ්යා ද පූර්ණ සංඛ්යා ද එකට එකක් අනුරූප වන අන්දමට මෙසේ ලියන්න. | ||
| − | + | 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 | |
| − | |||
| − | |||
| − | + | 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 | |
| − | |||
| − | + | 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| − | + | මේ පේළි දෙස බලන විට ඉරට්ට සංඛ්යාවක් ඊට අනුරූප ඔත්තේ සංඛ්යාවට එකක් වැඩි බව පෙනේ; එසේ ම ඊට අනුරූප පූර්ණ සංඛ්යාව මෙන් දෙගුණයක් වේ. | |
| − | + | 5ට අනුරූප ඉරට්ටෙට් සංඛ්යාව 6ය. පූර්ණ සංඛ්යාව 3ය. | |
| + | |||
| + | 6ට වඩා 5 එකකින් අඩුය. 6 = දෙවරක් 3 ව. මුල් ඔත්තේ සංඛ්යා හතේ ඓක්යය 7 x 7 වේ. මුල් ඉරට්ට සංඛ්යා හතේ ඓක්ය 7 x 7 + 7 වේ. එනම් 7 x 8 ය. | ||
| + | |||
| + | මෙසේ පළමුවැනි ඉරට්ටේ සංඛ්යා ගණනක ඓක්යය ඒ ගණන ඊළඟ සංඛ්යාවෙන් ගුණ කිරීමෙන් ලැබේ. පළමුවන පූර්ණ සංඛ්යා 7හි ඓක්යය මෙයින් ½ කි. | ||
| + | |||
| + | පළමුවන පුර්ණ සංඛ්යා 7හි ඓක්යය මෙයින් ඉරට්ට සංඛ්යා ද ඔත්තේ සංඛ්යා ද පූර්ණ සංඛ්යා ද එකතු කිරීමට මේ සුත්ර 3 ලැබේ. | ||
පළමුවැනි ඔත්තේ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය n x n වේ. | පළමුවැනි ඔත්තේ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය n x n වේ. | ||
| − | + | පළමුවැනි ඉරට්ට සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය n (n + 1) වේ. | |
පළමුවැනි පූර්ණ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය වේ. | පළමුවැනි පූර්ණ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය වේ. | ||
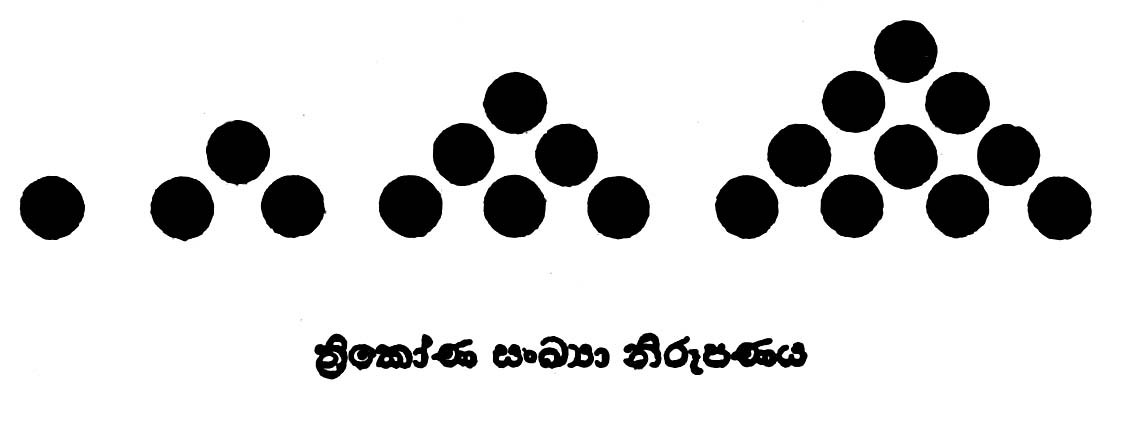
| − | + | එකේ සිට අනුගාමි සංඛ්යා ආකලන වශයෙන් එකතු කළ විට ලැබෙන ඓක්යය ශ්රේණීයට ත්රිකෝණ සංඛ්යා යයි කියනු ලැබේ. | |
| − | + | ||
| − | + | මෙසේ නම් කර තිබෙන්නේ මේවා ත්රිකෝණාකාරයට පිළියෙල කළ හැකි නිසාය. | |
| − | පුර්ණ සංඛ්යා : 1, 2, 3, 4, 5, 6, 7, 8 | + | [[ගොනුව:c-17.jpg|400px|left]] |
| − | ත්රිකෝණ සංඛ්යා : 1, 3, 6, 10, 15, 21, 28, 36 | + | '''පුර්ණ සංඛ්යා :''' 1, 2, 3, 4, 5, 6, 7, 8 |
| − | වර්ග සංඛ්යා : 1, 4, 9, 16, 25, 36, 49, 64 | + | |
| + | '''ත්රිකෝණ සංඛ්යා :''' 1, 3, 6, 10, 15, 21, 28, 36 | ||
| + | |||
| + | '''වර්ග සංඛ්යා :''' 1, 4, 9, 16, 25, 36, 49, 64 | ||
| − | එක ළඟ තිබෙන ත්රිකෝණ සංඛ්යා දෙකක් එකතු කිරීමෙන් වර්ග සංඛ්යා (Perfect number) : | + | එක ළඟ තිබෙන ත්රිකෝණ සංඛ්යා දෙකක් එකතු කිරීමෙන් වර්ග සංඛ්යා (Perfect number): 6හි එම සංඛ්යාව ම හැර අනික් සාධක 1, 2, 3 වේ. ඒවා එකතු කිරීමෙන් 6 ලැබේ. |
| − | අංගසම සංඛ්යා (Perfect numbers) : | + | '''අංගසම සංඛ්යා (Perfect numbers):''' 6හි එම සංඛ්යාව ම හැර අනික් සාධක 1, 2, 3 වේ. ඒවා එකතු කිරීමෙන් 628 ලැබේ. |
| − | + | 28හි 28 හැර අනික් සාධක 1, 2, 4, 7, 14 වේ. ඒවා එකතු කිරීමෙන් 28 ලැබේ. | |
6, 28 ආදි මෙවැනි සංඛ්යාවලට අංගසම සංඛ්යා යයි කියනු ලැබේ. | 6, 28 ආදි මෙවැනි සංඛ්යාවලට අංගසම සංඛ්යා යයි කියනු ලැබේ. | ||
| 305 පේළිය: | 372 පේළිය: | ||
496 ද 8128 ද වෙනත් මෙවැනි සංඛ්යා දෙකක් වේ. | 496 ද 8128 ද වෙනත් මෙවැනි සංඛ්යා දෙකක් වේ. | ||
| − | මිත්ර සංඛ්යා : | + | '''මිත්ර සංඛ්යා:''' 220හි එම සංඛ්යාව හැර එහි අනික් සාධක එකතු කළ විට 284 ලැබේ. 284 එම සංඛ්යාව හැර අනික් සාධක එකතු කළ විට 220 ලැබේ. මෙවැනි සංඛ්යාවලට මිත්ර සංඛ්යා යයි කියනු ලැබේ. |
දශම ක්රමයේ සංඛ්යාවලට තිබෙන ලක්ෂණ කිපයක් පහත දැක්වේ. | දශම ක්රමයේ සංඛ්යාවලට තිබෙන ලක්ෂණ කිපයක් පහත දැක්වේ. | ||
| 312 පේළිය: | 379 පේළිය: | ||
9 එකතු කිරීම ද, අඩු කිරීම ද පහසුය. 9 එකතු කිරීම අනික් සංඛ්යාවේ එකස්ථාන අංකයෙන් එකක් අඩුකර දශස්ථාන අංකයට එකක් එකතු කිරීමට සමානය: | 9 එකතු කිරීම ද, අඩු කිරීම ද පහසුය. 9 එකතු කිරීම අනික් සංඛ්යාවේ එකස්ථාන අංකයෙන් එකක් අඩුකර දශස්ථාන අංකයට එකක් එකතු කිරීමට සමානය: | ||
| − | |||
| − | |||
| − | + | 8 + 9 = 17 (8 හි දශමස්ථාන අංකය 0 ය.) | |
| − | |||
| − | II. දහයට අඩු පූර්ණ සංඛ්යාවක් 9 න් ගුණ කළ විට දක්නා ලද ලක්ෂණ අනුව අංක | + | 17 + 9 = 26 |
| − | + | ||
| − | + | සංඛ්යාවකින් 9ක් අඩුකිරීම ඒකස්ථාන අංකයට 1ක් එකතු කර දශස්ථාන අංකයෙන් 1ක් අඩු කිරීමට සමානය: | |
| + | |||
| + | 25 – 9 = 16 | ||
| + | |||
| + | II. දහයට අඩු පූර්ණ සංඛ්යාවක් 9 න් ගුණ කළ විට දක්නා ලද ලක්ෂණ අනුව අංක 2ක් තිබෙන සංඛ්යාවක් 99න් ගුණ කිරීම කළ හැකි ද කියා සෙවීම වටී. | ||
| + | |||
| + | 76 x 99 = 7524 76 – 1 = 75 | ||
| + | |||
| + | 75ත්, 24ත් 99 යි. | ||
මෙයත් සැබෑ බව පෙනේ. | මෙයත් සැබෑ බව පෙනේ. | ||
| − | + | 365 x 999 = 364635; මෙසේ ම 9999 න් අංක 4ක් තිබෙන සංඛ්යාවක් ද ගුණ කළ හැකිය. | |
| − | අංක | + | අංක 2ක් තිබෙන සංඛ්යාවක් ද මේ ක්රමයට 999න් ගුණ කළ හැකිය. සංඛ්යාවක අංක ගණන වමෙන් බින්දු ලියා වැඩි කළ හැකිය. 85 = 085 දැන් අංක තුනක් තිබේ. |
| + | |||
| + | 85 x 999 = 085 x 999 = 084915 | ||
| − | |||
එසේ ම 78 x 9999 = 00779922 = 779922 | එසේ ම 78 x 9999 = 00779922 = 779922 | ||
III. 1089 x 9 = 9801. ගුණ්යෙය අංක පරිවර්තනය කිරීමෙන් මෙය ලැබේ. 10989 x 9 = 98901. මේ ගුණිතය ද එසේ ම ගුණ්යයේ අංක පරිවර්තනය කිරීමෙන් ලැබේ. 1089 හි 0 ටත් 8 ටත් අතරේ 9 ඒවා කොපමණ ලියා බැලුවත් මෙය සත්යයක් බව පෙනේ. 109989 x 9 = 989901 | III. 1089 x 9 = 9801. ගුණ්යෙය අංක පරිවර්තනය කිරීමෙන් මෙය ලැබේ. 10989 x 9 = 98901. මේ ගුණිතය ද එසේ ම ගුණ්යයේ අංක පරිවර්තනය කිරීමෙන් ලැබේ. 1089 හි 0 ටත් 8 ටත් අතරේ 9 ඒවා කොපමණ ලියා බැලුවත් මෙය සත්යයක් බව පෙනේ. 109989 x 9 = 989901 | ||
| − | + | 10989 2 = 21978 | |
| − | |||
| − | + | 10989 2 = 87912 | |
| − | IV. 12345679 අපූරු සංඛ්යාවකි. මෙය | + | මේ ගුණිත දෙකින් එක ගුණිතයක් පරිවර්තනය කිරීමෙන් අනික ලැබේ. 3න් 7න් ගුණ කළත් 4න් 6න් ගුණ කළත් මෙවැනි ප්රතිඵල ම ලැබේ. |
| + | |||
| + | IV. 12345679 අපූරු සංඛ්යාවකි. මෙය 9යේ (90ට අඩු) ගුණාකාරයකින් ගුණකළොත් ගුණිතයේ එක ම අංකය ම ලැබේ. | ||
V. සංඛ්යා දෙකක දහයේ ඒවා ගණන සමාන නම්, එකස්ථාන අංක දෙක එකතු කළ විට 10 වේ. නම්, ඒ දෙක ගුණ කිරීම පහසුය. | V. සංඛ්යා දෙකක දහයේ ඒවා ගණන සමාන නම්, එකස්ථාන අංක දෙක එකතු කළ විට 10 වේ. නම්, ඒ දෙක ගුණ කිරීම පහසුය. | ||
| − | + | 87 83 = 7221 8 9 = 72 7 3 = 21 | |
| − | + | ||
| − | + | 95 95 = 9025 9 10 = 90 5 5 = 25 | |
| + | |||
| + | 116 114 = 13224 11 12 = 132 6 4 = 24 | ||
VI. සියස්ථාන අංකය එකස්ථාන අංකයට සම නොවූ අංක 3 ක් තිබෙන සංඛ්යාවක් ලියන්න. එහි අංක පරිවර්තනය කර ලැබෙන සංඛ්යාව පළමු සංඛ්යාවට වඩා වැඩි නම් ඊට උඩින් ද අඩු නම් ඊට යටින් ද ලියා අඩු කරන්න. | VI. සියස්ථාන අංකය එකස්ථාන අංකයට සම නොවූ අංක 3 ක් තිබෙන සංඛ්යාවක් ලියන්න. එහි අංක පරිවර්තනය කර ලැබෙන සංඛ්යාව පළමු සංඛ්යාවට වඩා වැඩි නම් ඊට උඩින් ද අඩු නම් ඊට යටින් ද ලියා අඩු කරන්න. | ||
| − | උදා . | + | උදා. 563 |
| − | - 365 | + | |
| + | -365 | ||
| − | 198 | + | 198 අන්තරයේ අංක ද පරිවර්තනය ද අන්තරයට |
| + | |||
| + | + 891 යටින් ලියා එකතු කරන්න. | ||
| + | |||
| + | 1089 | ||
| − | |||
| − | |||
පටන ගත සංඛ්යාව කුමක් වුවත් උත්තරය හැම විට ම 1089 වේ. | පටන ගත සංඛ්යාව කුමක් වුවත් උත්තරය හැම විට ම 1089 වේ. | ||
| − | VII. 8126 | + | VII. 8126 11න් ගුණ කරන්න. නැවත එම සංඛ්යාවේ අංක පරිවර්තනය කර 11න් ගුණ කරන්න. ගුණික දෙකේ අංක පරිවර්තනය වී ඇත. |
| − | + | ||
| − | + | 8126 11 = 89386 | |
| − | + | ||
| + | 6218 11 = 68398 | ||
| + | |||
| + | පළමුවැනි ගුණිතය පරිවර්තනය කිරිමෙන් දෙවැනි ගුණිතය ලැබේ. සංඛ්යාවක එක ළඟ තිබෙන අංක දෙකක ඓක්යය 10ට අඩු නම්, අංක කීයක් සංඛ්යාවේ තිබුණත් මේ ප්රතිඵලය හැම අවස්ථාවක දී ම ලැබෙනවා ඇත. | ||
| − | + | . 2 ද පුදුම ලක්ෂණ තිබෙන සංඛ්යාවකි. 1 + 2 + 3 + 4 + 8 + 16 + 32 ආදි වශයෙන් දෙකෙන් ගුණ කර ලැබෙන සංඛ්යා ලිවීමෙන් සංඛ්යා දෙකේ ඓක්යය තුන්වැනි සංඛ්යාවට එකක් අඩුය. පළමුවැනි සංඛ්යා තුනේ ඓක්යය සතරවැන්නට එකක් අඩුය. මේ ක්රමයට මේ සංඛ්යා එකතු කළ හැකිය. | |
| − | මැජික්ප | + | '''මැජික්ප කොටු:''' කුඩා හතරැස් කොටු 9ක් තිබෙන හතරැස් කොටුවක අනුගාමි සංඛ්යා 9ක් හරස් අතට ද සිරස් අතට ද කොනින් කොනට ද එනම් විකර්ණයක් දිගේ ද එකතු කළ විට ඓක්යය සම වන සේ ලිවිය හැකිය. 1 සිට 9 දක්වා තිබෙන අනුගාමි සංඛ්යා මේ කොටුවේ මෙසේ ලියා තිබේ. |
8 1 6 | 8 1 6 | ||
| + | |||
3 5 7 | 3 5 7 | ||
| + | |||
4 9 2 | 4 9 2 | ||
මෙවැනි කොටුවලට මැජික් කොටු යයි කියනු ලැබේ. | මෙවැනි කොටුවලට මැජික් කොටු යයි කියනු ලැබේ. | ||
| − | එසේ ම අනුගාමි සංඛ්යා | + | එසේ ම අනුගාමි සංඛ්යා 16ක්, 25ක් 36ක් 49ක් ආදි වශයෙන් මෙසේ මැජික් කොටුවල ලිවිය හැකි |
| + | |||
| + | 17 24 1 8 15 | ||
| + | |||
| + | 23 5 7 14 16 | ||
| + | |||
| + | 4 6 13 20 22 | ||
| + | |||
| + | 10 12 19 21 3 | ||
| + | |||
| + | 11 18 25 2 9 | ||
| + | |||
| + | මේ මැජික් කොටු ගැන භාරත දේශියයන් අවුරුදු දෙදහකට පෙර දැන ගෙන සිටි බවට සාක්ෂ්ය තිබේ. පළමු අංක 16 පුදුම විදිහට ලියා තිබෙන මැජික් සමචතුරස්රයක් ඉන්දියාවේ ග්වාලියෝර් නගරයේ කොටුවට ඇතුළුවන ස්ථානයේ කුලුනක කපා තිබේ. එම මැජික් කොටුව මෙහි දැක්වේ.:- | ||
| + | |||
| + | 15 10 3 6 | ||
| − | + | 4 5 16 9 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 14 11 2 7 | |
| − | + | 1 8 13 12 | |
| − | |||
| − | |||
| − | |||
| − | + | මෙහි හරහට හා පහළට පමණක් නොව සියලු ම විකර්ණ දිගේ තිබෙන සංඛ්යා ද එකතු කළ විට 34 ලැබේ. | |
| − | + | එපමණක් නොව මෙහි තිබෙන සියලු ම සම චතුරස්රවල කොන්වල තිබෙන කොටු හතරේ සංඛ්යා එකතු කළ විට ද 34 ලැබේ. | |
| − | කර්තෘ:පී. ද ඇස්. කුලරත්න | + | කර්තෘ:[[පී. ද ඇස්. කුලරත්න]] |
(සංස්කරණය:1963) | (සංස්කරණය:1963) | ||
[[ප්රවර්ගය:අ]] | [[ප්රවර්ගය:අ]] | ||
15:16, 11 ජූලි 2023 වන විට නවතම සංශෝධනය
අංක හෙවත් ඉලක්කම් මගින් ප්රකාශ කෙරෙන සංඛ්යා, ඒවා භාවිත කරන පිළිවෙල සහ එම සංඛ්යාවන්ගෙන් ලක්ෂණ (properties) උගන්වන්නාවූ විද්යාව අංක ගණිතය නම් වේ. අංක ගණිතයේ ගණන් බැලීම්වල දී භාවිතා වන ක්රම පිළිබඳ දෘඪ සාධන අනපේක්ෂිතය.
සංඛ්යා යන්නෙහි අදහස කුමක්ද?
අංක හෙවත් ඉල්ලකම් යි කියනු ලබන්නේ මොනවාදැයි යනු මෙහි ලා නැගෙන ප්රශ්න දෙකකි.
කවුද, කොහොමද, කොහේ ආදි ප්රශ්නවලට උත්තර දීම සඳහා මිනිසා සාමාන්ය භාෂාව යොදා ගනී. එසේ වුව ද කීය ද කොපමණ ද ආදී ප්රශ්නවලට උත්තර දීම සදහා මිනිසාට තමන්ගේ සමාන්ය භාෂාවට අමතර වශයෛන් අලුත් වචන නිපදවා ව්යවහාර කිරීමට සිදුවිය. ජිවිතයේ සියලු අවස්ථාවන්හිදී ම මේ අන්දමේ ප්රශ්න ඉදිරිපත් වන නිසා භාවිතයෙහි යෙදෙන භාෂාවට අලුත් වචන යොදාගන්ට වීමෙන් ගණිතමය භාෂාවක් ද ඇති විය. කීය ද කොපමණ ද ආදි ප්රශ්නවලට උත්තර සැපයෙන්නේ සංඛ්යා මගිනි.
"න මානෙන විනා යුක්තිර්
ද්රව්යානාං ජායතෙ ක්වවිත්" (මැනුමක් කිරුමක් නැතිව ද්රව්යයන්ගේ ව්යවහාරයෙන් කිසිවිටෙක නොවන්නේ ය.) යනු පැරණි පණ්ඩිත මතයකි. මනුෂ්යාගේ එදිනෙදා කටයුතුවලදී තමන්ට අයිති දේ කොපමණ දැයි බලාගැනීමට මැනුම හා කිරුම අවශ්ය මය. කිරුමෙන් හා මැනුමෙන් ලැබෙන ප්රතිඵලය සටහන් කර තැබීම ද වැදගත් ය. ඒ නිසා හරකකු හෝ බැටළුවකු අයිති මිනිසා තමාට අයිති හරකුන් හෝ බැටළුවන් ගණන හැඳින්වීමට එක යන වචනය යොදා ගත්තේ ය. තව එකෙක් සිටි නම් දෙක යන වචනය ද, මෙසේ එක එකා වැඩිවන විට තු , හතර, පහ ආදි වචන ද යොදා ගැනීමට සිදුවිය. ඒ ඒ රටවල මිනිසුන් එක, දෙක, තුන, ආදි වචන වෙනුවට අනුරූප වචන යොදා ගෙන තිබේ.
ද්රව්ය සමුහයක තිබෙන ද්රව්ය ගණන කීයදැයි සෙවීම ගණන් කිරීම නම් වේ. ගණන් කිරීමෙන් ලැබෙන සංඛ්යාවලට පුර්ණ සංඛ්යා, ප්රකෘති සංඛ්යා යන නම් දී තිබේ. වඩාත් නිවැරදි ලෙස ගණිත භාෂාවෙන් කියතොත් මේ සංඛ්යා ධනපූර්ණ සංඛ්යා නම් වේ.
සංඛ්යා භාවිත කිරීමේ දී ප්රධාන ගණිත කර්ම සතරක් තිබේ. එනම් එකතු කිරීම, අඩු කිරීම, ගුණ කිරීම, බෙදීම යනුයි.
පටුන
එකතු කිරීම සහ අඩු කිරීම:
එක් ද්රව්ය සමුහයක ද්රව්ය අටක් ද, වෙනත් ද්රව්ය සමූහයක ද්රව්ය පහක් ද තිබේ නම් මුළු ද්රව්ය ගණන 13 ක් වේ. 8 ටෙන් 5 හෙන් මුළු ගණන 13 වේ. සංඛ්යා දෙකක හෝ වැඩි ගණනක මුළු ගණනට ඓක්යය හෝ එකතුව යයි කියනු ලැබේ. මෙහි දී පාව්චිචි කරන ගණිත කර්මය එකතු කිරීම වේ. "+" ලකුණ එකතු කිරීමේ ලකුණය. මෙහි නම ධන යනුයි.
8 + 5 = 13ය; මෙය කියවන්නේ, අට ධන පහ සමානයි දහතුන කියාය.
බඩු ගොඩවල් දෙකක තිබෙන මුත් මුළු බඩු ගණන සෙවීමේ දී පළමු ගොඩෙන් පටන්ගෙන ගණන් කළත්, දෙවෙනි ගොඩෙන් පටන් ගෙන ගණන් කළත් ලැබෙනක ප්රතිඵලය සමාන බව පැහැදිලිය.
8 + 5 = 13; 5 + 8 = 13
සංඛ්යා එකතු කිරීමේ ගණිත කර්මයේ දී එක ම අනුපිළිවෙළකට සංඛ්යා ලිවීම අවශ්ය නොවේ. එම නිසා පහත සඳහන් මූලික න්යාය දෙක එකතු කිරීමේ ගණිත කර්මයට බලපායි.
01) එකතු කිරීමේ පරිවර්තන න්යාය:
a + b = b + a
02) එකතු කිරීමේ සංඝටන න්යාය:
a + (b + c) = (a + b) + c
මෙහි a, b, c යන සංකේතවලින් සංඛ්යා හඳුන්වනු ලැබේ.
13න් 8ක් අඩු කළ විට 5ක් ද, එසේ ම 13න් 5ක් අඩු කළ විට 8ක් ද ඉතිරි වේ. මේ ගණිත කර්මය අඩුකිරීම වේ.
"-" ලකුණ අඩු කිරීමේ ලකුණයි. මෙහි නම සෘණ යනුයි.
එක සංඛ්යාවකින් තවත් සංඛ්යාවක් අඩු කළ විට ලැබෙන සංඛ්යාවට අන්තරය යයි කියනු ලැබේ. මෙකී සිද්ධි මෙසේ පෙන්විය හැක;
8 + 5 = 13
5 + 8 = 13
13 - 5 = 8
13 - 8 = 5
8, 5, 13 යන සංඛ්යා තුන වෙනුවට a, b, c සංකේත පාව්ච්චි කර මෙම සිද්ධි පොදු වශයෙන් මෙසේ පෙන්විය හැකිය. a සහ b එකතු කළ විට ඓක්යය c ය.
a + b = c
b + a = c
c – a = b
c – b = a
අඩු කිරීම එකතු කිරිම් මගින් ද දැක්විය හැක. 13න් 5ක් අඩු කිරීම 5ට කීයක් එකතු කළ විට 13ක් ලැබේ ද යන ප්රශ්නය මතය.
එක දොඩම් ගෙඩියක් තිබෙන තැනට තව දොඩම් ගෙඩියක් දැමූ විට ඒ ගොඩේ දොඩම් ගෙඩි දෙකක් වේ. 1ට 1ක් එකතු කළ විට 2 ලැබේ. මෙසේ 2ට තව එකක් එකතු කිරීමෙන් 3 ද, 3ට තව එකක් එකතු කිරීමෙන් 4 ද ආදි වශයෙන් ලැබෙන නිසා, ගණන් කිරීම එකතු කිරීමක් බව පැහැදිලි වේ.
ගුණ කිරීම:
එක ම සංඛ්යාව කීපවාරයක් ගෙන එකතු කිරිමෙන් ඓක්යය ලබාගැනීම වෙනුවට එය ලබාගැනීමේ විශේෂ ක්රමයක් ඇත. 7 + 7+ 7 + 7 යන්න කෙටිකර මෙසේ ලිවිය හැක: 7 x 4 මේ ගණිත කර්මයට ගුණකිරීම යයි කියනු ලැබේ. මෙහි 7ට ගුණ්යය යයි ද එකතු කිරීමට තිබෙන සංඛ්යාවේ වාර ගණන පෙන්වන 4ට ගුණකයයි ද, ගුණ කිරීමෙන් ලැබෙන ප්රතිඵලයට ගුණිතයයි ද කියනු ලැබේ. ලකුණ "X" ගුණ කිරීමේ ලකුණයි. එක කියවන්නේ වරක් කියායි. දෙවරක්, තුන්වරක් ආදි ගුණකිරීමේ වක්ර ගුණිතය සෙවීමට පිහිට වේ.
පේළියටකට ගඩොල් කැට 7ක් බැගින් තිබෙන සේ තිරස් පේළි 4ක් මෙසේ පිළියෙල කළ හැකිය. එවිට සිරස් පේළියක ගඩොල් කැට සතරක් තිබේ. මෙහි ගඩොල් කැට 7 බැගින් තිබෙන තිරස් පේළි 4ක් ද එසේ ම ගඩොල් කැට 4 බැගින් තිබෙන සිරස් පේළි 7ක් ද තිබේ. මුළු ගඩොල් ගණන 7 x 4 ට ද 4 x 7ට ද සමාන වේ. එම නිසා 7 x 4 = 4 x 7 ගුණ කිරීමක දී ගුණ්යය ද ගුණකය ද එක ම අනුපිළිවෙලකට ලිවීම අනවශ්යය. ගුණ කිරීමේ දී මේ වැදගත් තුන්වැනි ගණිත න්යාය බලපාන බව පැහැදිලිය.
(3) ගුණකිරීමේ පරිවර්තනය න්යාය: a x b = b x a 7 x 4 = 28 මෙහි ගුණ්යය වූ 7ට ද ගුණකය වූ 4ට ද 28 ටේ සාධක යයි කියනු ලැබේ. සාධක තිබෙන නිසා 28 සාධක සංඛ්යාවක් යයි කියනු ලැබේ.
ඉහත පෙන්වන ලද ගඩොල් තිරස් පේළි 4රේ තිබෙන එක එක ගඩොල් කැටය උඩ තව ගඩොල් කැටය උඩ තව ගඩොල් කැට 2 බැගින් තබමු. එවිට තිරස් පේළියක තිබෙන ගඩොල් ගණන 3 x 7 වේ. එවැනි පේළි 4ක් තිබෙන නිසා මුළු ගඩොල් ගණන (3 x 7) x 4 ය. එක ගොඩක ඇති ගඩොල් ගණන 3කි. මෙවැනි ගොඩවල් තිරස් පේළියක 7 බැගින් ද සිරස් පේළියක 4 බැගින් ද ඇත. එබැවින් මුළු ගඩොවල් ගණන 7 x 4 වේ. ඒ නිසා මුළු ගඩොල් කැට ගණන 3 x (7 x 4) වේ. (3 x 7) x 4 = 3 x ( 7 x 4).
අංක ගණිතයේ හතර වැනි වැදගත් න්යාය වූ මෙය පොදු වශයෙන් මෙසේ ලිවිය හැක:
04) ගුණ කිරීමේ සංඝටන න්යාය: (a x b) x c = a x (b x c )
පළමුවෙන් පිළියෙල කරන ලද ගඩොල් කැට 28 කීප විදියකට දෙකොසකට වෙන් කළ හැකිය. එයින් එකක් ගනිමු. සිරස් පේළි 2ක් එක කොටසකට ද 5ක් අනික් කොටසට ද වෙන් කරමු. එවිට පළමුවැනි කොටසේ ගඩොල් කැට 2 x 4ක් ද අනික් කොටසේ 5 x 4ක් ද තිබේ. එහි තිබෙන මුළු ගඩොල් කැට ගණන 2 x 4 + 5 x 4 වේ. එම නිසා 7 x 4 හෙවත් (2 + 5) x 4 = 2 x 4 + 5 x 4.
මේ පස්වැනි න්යාය ද අංක ගණිතයේ වැදගත් න්යායක් වේ. එය පොදු වශයෙන් මෙසේ ලිවිය හැක:
05) ගුණ කිරීමේ විඝටනය න්යාය: ( a+ b) x c = a x c + b x c
එකම සංඛ්යාව කිප වරක් ලියා එකතු කිරීම කෙටිකර ගුණ කිරීමක් මෙන් ලියන්නට හැකිවා මෙන් ම, එක ම සංඛ්යාව කීප වරක් ගුණ කිරිමෙන් ලැබෙන අඛණ්ඩ ගුණිතය ද කෙටිකර ලිවීමට ක්රමයක් තිබේ.
උදා: 6 x 6 x 6 = 63 මෙහි 6 ට උඩින් දකුණු පැත්තෙන් ලියා තිබෙන 3ට දර්ශකය යි කියනු ලැබේ. මෙහි ගුණිතය 6 යේ 3 වෙනි බලය වේ. දර්ශකය ගුණිතයේ බලයේ තිබෙන සාධක ගණන පෙන්වයි. දර්ශක වාදයෙහි අංක ගණිතයට අවශ්ය වූ වැදගත් න්යාය 4ක් තිබේ. a, b, m, n යන සංඛ්යා සතර ධනපුර්ණ සංඛ්යා වේ නම්, මේ න්යාය සතර මෙසේ ලවිය හැකිය:
am x an = am+n උදා . 63 x 62 = 65
(am) n = am n උදා . (52) 3 = 56
(a x b)m = a x bm
උදා . (3 x 4)2 = 32 x 42
m යන සංඛ්යාව n යන සංඛ්යාවට වඩා ලොකු නම් am ÷ an = an = am –n
උදා. 75 ÷ 72 = 73
බෙදීම:
7 x 4 = 28; 28, 4න් බෙදු විට 7 ලැබේ. මෙය ලියන්නේ මෙසේය: 28 ÷ 4 = 7 "÷" බෙදීමේ ලකුණය. මෙහි 28ට භාජ්යය යයි ද 4ට භාජකය යයි ද 7ට ලබ්ධිය යයි ද කියනු ලැබේ. 28ට වනාහි 7හි සහ 4හි ද ගුණාකාරයකි. 28 ÷ 4 යන්නෙහි තේරුම 28 කින් 4 ගොඩවල් කී වරක් අඩු කළ හැකිද? මෙය ගුණ කිරීමේ ප්රතිවිරුද්ධ අදහසය. 7 x 4 යන්නෙහි තේරුම 7 ඒවා 4ක් එකතු කළ විට කීයක් ලැබේ ද යන්නය.
පොදු වශයෙන් a x b = c නම් c ÷ a = b; c ÷ b = a; c යනු a හි ද b ද ගුණාකාර වේ.
a සහ b සංඛ්යා දෙකක් වේ නම් a, bට වඩා කුඩා විය හැකිය; නැතහොත් a, bට සමාන විය හැකිය; එසේත් නැතහොත් a, bට වඩා ලොකු විය හැකිය. මෙය සංකේත මගින් ප්රකාශ කරන්නේ මෙසේය.
a < b a , b ට වඩා කුඩාය.
a = b a , b ට සමානය.
a > b a , b ට වඩා ලොකුය.
a > b නම්, b වලින් a බෙදු විට ලබ්ධියක් ද ශේෂයක් ද ලැබේ.
උදා:- 57 ÷ 6 ; ලබ්ධිය 9 වේ. ශේෂය 3 ය.
57 = 6 x 9 + 3
හැම සංඛ්යාවක් ම ඊට කුඩා සංඛ්යාවකින් බෙදු විට මේ අන්දමට ලබ්ධිය වූ ද, ශේෂය වූ ද පූර්ණ සංඛ්යා දෙකක් ලබාගත හැක. ශේෂය බින්දුව (0) නම් ලොකු සංඛ්යාවෙන් බෙදිය හැකි යයි කියනු ලැබේ.
1, 1න් ගුණ කළවිට ගුණිතය 1 ය. 1, 1න් බෙදුවිට ලබ්ධිය 1 ය. 1 සියලු ම පූර්ණ සංඛ්යා වන්ගේ සාධකයෙකි. සංඛ්යාවක් 0න් ගුණ කළ විට ගුණිතය 0 වේ. බින්දුව බින්දුවෙන් බෙදීම නිරර්ථකය. හැම සංඛ්යාවක් ම 1න් ද එම සංඛ්යාවෙන් ම ද බෙදිය හැක. 1 x 3 = 3; 1 x a = a සංඛ්යාවකට 1ත් එම සංඛ්යාවත් හැර වෙන සාධක නැති නම් ඊට මූලසංඛ්යා යයි කියනු ලැබේ. සාමාන්යෙයන් 1 මුලසංඛ්යා යයි කියනු ලැබේ. සාමාන්යයෙන් 1 මූලසංඛ්යාවක් හැටියට සලකන්නේ නැත. නමුත් සමහර විට එය ද මූලසංඛ්යා ගණයට අයත් කොට ගනු ලැබේ. 2, 3, 5, 6, 7, 11, 13 ආදිය මූල සංඛ්යාවෝයි.
සංඛ්යා වාදය අංක ගණිතයේ උසස් ම කොටසකි. මුලසංඛ්යා ගැන සංඛ්යාවාදයේ ප්රමේයයන් කීපයක් තිබේ. එයින් එකක් නම් සැම සාධක සංඛ්යාවක් ම මූලසංඛ්යාවල ගණිතයක් සේ ප්රකාශ කළ හැකිය යනුයි. සාධකවල පිළිවෙල නොසලකනවා නම් මෙය කළ හැක්කේ එක ම ආකාරයෙනි.
උදා: 36 = 4 x 9 = 22 x 32
සාධක සංඛ්යා දෙකක් හෝ ඊට වැඩි ගණනක් ගනිමු. මේ සංඛ්යා සියල්ල ම බෙදිය හැකි ලොකු ම සාධකයක් තිබේ.
උදා: 28 = 22 x 7
42 = 2 x 3 x 7
2 ද 7 ද , 28ටේත්, 42කේත් පොදු සාධක වේ. 14 මේ සංඛ්යා දෙකේ ලොකු ම පොදු සාධකයයි. සංඛ්යා ගණනක ලොකු ම පොදු සාධකයට මහා සාධකයයි කියනු ලැබේ.
එසේ ම සංඛ්යා කීපයකින් බෙදිය හැකි ඒ සංඛ්යාවල කුඩා ම ගුණාකාරයන් තිබේ. එයට කුඩා ම පොදු ගුණාකරයයි කියනු ලැබේ. 28ටේන් 42කේත් කුඩා ම පොදුගුණාකාරය 22 x 3 x 7 එනම් 84 වේ.
a යනු bට වඩා ලොකු සංඛ්යාවක් නම් a = b x q + r මෙහි q ලබ්ධිය වේ. r ශේෂය වේ. bට වඩා r කුඩාය. a සහ bහි පොදු සාධකයක් වේ. මෙසේ a සහ b යන සංඛ්යා දෙකේ මහා පොදු සාධකය b සහ r යන සංඛ්යා දෙකේ මහාපොළ සාධකයට සමානය. ශේෂය වූ r යන්නෙන් b බෙදීමෙන් මෙය ලැබේ.
b = r x p + s
දැන් b සහ rහි මහාපොදු සාධකය r සහ sහි මහාපොදු සාධකයට සමානය. මෙසේ ශේෂයෙක් නැතිවන තුරු ශේෂයෙන් භාජකය බෙදීමෙන් සංඛ්යා දෙකක මහාපොදු සාධකය සෙවිය හැකි මේ ක්රියාවලියෙහි දී ලැබෙන අවසාන පූර්ව ශේෂය සංඛ්යා ද්වයේ මහාපොදු සාධකයයි.
භාග:
a ÷ bයන් බෙදීමකි. එය මෙසේ ද ලිවිය හැක: මෙය කියවන්නේ aයට b කියාය. මේ ආකාරයට ලියන ලද බෙදීමට හැටියට සලකන විට භාජ්යය වූ aට, භාගයක් හැටියට සලකන විට ලවයයි කියනු ලැබේ. භාජකය වූ bට හරයයි කියනු ලැබේ. a ÷ b බෙදීමෙන් ලැබෙන සම්පූර්ණ ලබ්ධිය යන භාගයෙන් හැඳින්වේ.
උදා. = 4; හි සම්පූර්ණ ලබ්ධිය 4 වේ. නමුත් 25 ÷ 7හි ලබ්ධිය 3 වේ. 4 වූ ශේෂයක් ලැබේ.
ඉහත පෙන්වූ ආකාරයෙන් 25 ÷ 7 යන බෙදීමේ සම්පූර්ණ ලබ්ධිය මෙන් පෙන්විය හැකිය.
=; මේ බෙදීමේ සම්පූර්ණ ලබ්ධිය වේ. මෙය ලියන්නේ මෙනි.
භාගය කියන්නේ සංඛ්යාවකින් කොටසකටය. යමක් සමාන කොටස් දෙකකට බෙදු විට ලැබෙන කොටසට හෙවත් භාගයට එයින් බාගයයි කියනු ලැබේ. 1, 2 බෙදු විට ලැබෙන්නේ බාගයයි. එනම් යි.
මැනිමේ සහ කිරීමේ දී සියලු දේ ම ඒකක සම්පූර්ණ ගණනකින් මැනිය හෝ කිරිය නොහැකිය. බාල්කයක දිග අඩිවලින් මනින විට එහි තිබෙන අඩි ගණන සංඛ්යාවකින් පමණක් සම්පූර්ණයෙන් මැනීමට නොහැකිවන්නට පුළුවන.
බාල්කයක දිගෙහි සම්පූර්ණ අඩි 12ක් ද අඩියකට අඩු කොටසක් ද තිබිය හැකිය. බර කිරීමේ දී ද එසේ මය. අඩියට අඩු කොටස මැනීමට අඩිය සමාන කොටස් 12කට බෙදා එක කොටසකට අඟල යයි කියනු ලැබේ. එසේම බර කිරීමේ දී රාත්තලට අඩු කොටස මැනීමට අවුන්ස යයි කියන සමාන කොටස් 16කට රාත්තල බෙදා තිබේ.
බාල්කයක දිග අඩි 8 අඟල් 5 කියනවා වෙනුවට එහි දිග අඩි කියා දැක්විය හැකිය. අඟලක් අඩියකින් දොළහෙන් පංගුවය.; අඟල් 1 = අඩි අඟල් 5 එවැනි කොටස් 5; අඟල් 5 = අඩි භාගයක ලවය හරයට අඩු නම් ඊට නියම භාග යයි ද අනික් භාගවලට විෂම භාග යයි ද කියනු ලැබේ. භාගවල හරය සම නම් භාග එකතු කිරීම ද අඩු කිරීම ද පහසුය.
උදා. න් පංගු තුනක් ද පංගු දෙකක් ද එකතු කළ විට 7න් පංගු 5ක් ලැබේ.
න් කොටසක් 4කින් එවැනි කොටස් 2ක් අඩු කළ විට 7න් කොටස් 2ක් ලැබේ.
යන භාගයේ හරයට හා ලවයට ද පොදු සාධක නැත. එවැනි භාග කුඩා ම ස්වරූපයෙන් ලියා තිබේ. භාගයක ලවය ද හරය ද එක ම සංඛ්යාවෙන් ගුණ කිරිමෙන් හෝ බෙදීමෙන් භාගයේ වටිනාකම වෙනස් නොවේ.
උදා. ; මෙහි හරය ද ලවය ද 2න් ගුණ කර තිබේ.
- මෙහි හරය ද ලවය ද 3න් බෙදා තිබේ.
- අඟල් 4ක් 6ට බෙදුවත් අඟල් 2ක් තුනට බෙදුවත් ලැබෙන දිග ප්රමාණය සමානය. භාගවල හර වෙනස් වූ විට ඒවා සමාන හරයක් සහිත භාගයකට පෙරලීමෙන් ඒ සියලු ම භාග එකතු කිරීම ද අඩු කිරීම ද කළ හැක.
උදා.
භාග දෙකක් ගුණ කරන්නේ මෙසේය.
න් ගුණ කිරීම වෙනුවට 2න් ගුණ කළහොත් ලැබෙන ගුණිතය 5 ගුණයක් ලොකුය. මන්ද? , 2න් පහෙන් පංගුව නිසාය. එම නිසා න් ගුණ කිරීමට 2න් ගුණ කර ලැබෙන ගුණිතය 5න් බෙදිය යුතුය.
න් නේ පරස්පරය යයි කියනු ලැබේ. භාගයක පරස්පරයක් ලබාගැනීමට ලවය හරය කර හරය ලවය කර භාගය ලිවිය යුතුය. භාගයක් භාග යෙකින් බෙදීමට පරස්පරයෙන් ගුණ කළ යුතුය.
න් බෙදනවා වෙනුවට එය 2න් බෙදුවොත් භාජකය 5 ගුණයක් අඩු වන නිසා 2න් බෙදු විට ලැබෙන ලබ්ධිය 5න් ගුණ කළ යුතුය.
එම නිසා
දශම භාග:
1ට අඩු සංඛ්යා නියම භාග මෙන් පමණක් නොව තවත් ක්රමයකට ද ලිවිය හැක. එනම්, පූර්ණ සංඛ්යාවන් පිළිබඳ ස්ථානීය අගය සුත්රයේ අනුසාරයෙන් දශම ක්රමයෙන් ප්රකාශ කළ හැකිය. අඩියකට අඩු කෑල්ලක් ඉතිරි වේ නම්, එය අඟල්වලින් මනිනවා වෙනුවට අඩිය සම කොටස් 10කට බෙදා එවැනි කොටස් කීයකට එහි දිග සමාන දැයි සෙවිය හැකිය. අඩි ගණන 17යි කියා ගනිමු. අඩියට අඩු කෑල්ලේ අඩියෙන් 10න් පංගු 3ක් තිබුණ හැටියට ගනිමු. අඩියෙන් 10න් පංගුවකට අඩු තවත් කෑල්ලක් තිබේ නම් අඩියෙකන් සම කොටස් 100කට බෙදා එවැනි කොටස් කීයක් ඉතිරි කොටසේ තිබේ දැයි සෙවිය හැකිය. එවැනි කොටස් 7ක් තිබුණි නම් බාල්කයේ දිග අඩි යි. තවත් කොටසක් ඉතිරි වේ නම් කොටසක් සම කොටස් 10කට බෙදා එනම් අඩියෙන් 1000න් පංගු ගෙන එහි එවැනි කොටස් කීයක් තිබේ දැයි සෙවිය හැකිය. මෙසේ ආදි කොටස්වලට අඩිය බෙදීමෙන් බාල්කයේ දිග දශම ක්රමයෙන් ප්රකාශ කළ හැකිය.
මේ දශම ක්රමය පුර්ණ සංඛ්යා ලියන ක්රමය පුළුල් කිරීමකි. 3857 දශම ක්රමයට ලියන ලද සංඛ්යාවක් නම් එහි වටිනාකම මේ අන්දමට ලිවිය හැකිය. 3857 = 3 x 103 + 8 x 102 + 5 x 10 +7
දැන් මේ සංඛ්යාවේ 1000 ඒවා වෙන්කර ඊට පසු 100 ඒවා වෙන්කර ඊට පසුව 10 ඒවා වෙන්කර ඊට පසුව 1 ඒවා ලබාගෙන තිබේ. දැන් 1ට අඩු කොටසක් තිබේ නම් එහි ඒවා වෙන්කර ඉතිරි කොටසේ ඒවා වෙන්කර එසේම ඒවා ඒවා ආදි වශයෙන් වෙන්කර සංඛ්යාවේ වටිනාකම ලිවිය හැකිය.
යන සංඛ්යාව මෙසේ ප්රකාශ කරන විට හි ඒවා කොපමණ තිබේ දැයි සෙවිය යුතුය. හි ඒවා ක් හෙවත් ඒවා 1ක් ද ඒවායින් ක්ද තිබේ. ඒවා හි ඒවා හෙවත් තිබේ. ඒවා හි ඒවා 5ක් තිබේ. එම නිසා මෙය සථානීය අගය යන සුත්රය අනුව මෙසේ ලියනු ලැබේ: = 14.125 මෙහි 4ටත් 1ටත් අතර තිබෙන තිතට දශම තිත යයි කියනු ලැබේ. එය ලියන්නේ මැදට ටිකක් උඩින්ය. එයින් එකේ ඒවා ගණන ඒවා ගණනින් වෙන්කර දැක්වේ.
පූර්ණ සංඛ්යාව ද දශම භාග ද ස්ථානීය අගය සුත්රය අනුව ලියන ලද සංඛ්යා නිසා, මේ සංඛ්යා එකතු කරන්නේ ද අඩු කරන්නේ ද එක ම ක්රම යෙනි. එනම්, ස්ථානීය අගය සම වූ සංඛ්යා එක යට එක ලිවීමෙනි.
පුර්ණ සංඛ්යාවකින් ගුණ කරන්නේ ගුණ කිරීමේ චක්ර මගින් බව කලින් කියා ඇත. සංඛ්යාවක් 357 වැනි ලොකු සංඛ්යාවකින් ගුණ කරන විට පළමුව 300න් ද දෙවනුව 50න් ද තුන්වෙනුව 7න් ද ගුණකර ලැබෙන ගුණිතයන් එකතු කර සම්පූර්ණ ගුණිතය ලබාගත හැකිය.
දශම භාග ගුණකිරීමේ දී දශම තිත නොසලකා පූර්ණ සංඛ්යා මෙන් ගුණකර ගුණිතයේ දශමස්ථාන ගණන ගුණයේ ද ගුණකයේ ද තිබෙන දශමස්ථාන ගණන්වල ඓක්යයට සමාන වන සේ දශම තිත තැබීමෙන් නිවැරදි ගුණිතය ලබාගත හැකිය.
සංඛ්යාවකින් බෙදීම:
10න් හෝ 10ට අඩු සංඛ්යාවකින් බෙදන විට එය කෙටි ක්රමයෙන් කළ හැකිය. 9න් 6745 බෙදීම යනු 9 ඒවා කීයක් එකතු කළ විට 6745 ලැබේ ද නැතහොත් 6745න් 9 ඒවා කීයක් අඩුකළ හැකි ද යන්න සෙවීමයි. 6745හි තිබෙන්නේ 1000 ඒවා 6කි. එම නිසා 6745හි තිබෙන 9 ඒවා ගණන 1000ට අඩුය. 6745හි 100 ඒවා 67ක් තිබේ. 67, 9 බෙදීමෙන් 6745න් 9 ඒවා 700ක් අඩු කළ හැකි බව පෙනේ. ඉතිරි වන්නේ 445යි. 445ට දහයේ ඒවා 44කි. 9න් 44 බෙදීමෙන් 445න් 9 ඒවා 40ක් අඩු කළ හැකි බව පෙනේ. ඊට පසු ඉතිරිවන 85න් 9 ඒවා 9ක් කළ විට 4ක් ඉතිරි වන බව පෙනේ. එම නිසා 6745න් 9 ඒවා 749ක් අඩුකළ හැකිය. 4ක් ඉතිරි වේ. මෙම බෙදීම ලියන්නේ මෙසේය.
9 6745 හෝ 6745 = 749
749 - 4 9
10ට වඩා ලොකු සංඛ්යාවකින් බෙදීම කරන්නේ ද මේ අන්දමටය.
45237 , 57න් බෙදීමේ දී භාජ්යයේ තිබෙන 10,000 ඒවා ගණන වත් 1000 ඒවා ගණන වත් 57න් බෙදිය නොහැකි බව පෙනේ. එම නිසා පළමුව 100 ඒවා ගණන වූ 452 ගෙන එහි 57 ඒවා කීයක් තිබේ දැයි බැලිය යුතුයි. ඒ ගණන 100 ඒවායෙන් අඩුකර ඉතිරි ගණන 57න් බෙදිය යුතුයි.
මේ බෙදීම කරන්නේ මෙසේයි.
793 100 ඒවා 452න් 57 ඒවා 7ක් අඩු කළ හැකිය. ඉතිරි වන්නේ 10 ඒවා 533 කි. එයින් 57 ඒවා
57 45239 9ක් අඩු කළ හැකිය. එම නිසා ලබ්ධියේ දශස්ථානයට 9 ලැබේ. දැන් ඉතිරි වන්නේ 209යි.
399 මෙයින් 57 ඒවා 3ක් අඩු කළ විට 38ක් ඉතිරි වේ.
533
513
209
171
38
දශම භාග බෙදීමේ දී භාජකය පුර්ණ සංඛ්යාවක් කර මේ අන්දමට ම බෙදීම කළ හැකිය. දශම භාගයක් පූර්ණ සංඛ්යාවක් කරනුයේ 10න් හෝ 100න් හෝ 1000න් හෝ 10යේ අන්කිසි බලයකින් ගුණ කිරීමෙනි. 10යේ බලය භාගයේ දශමස්ථාන ගණනට සමානය.
3.57 100 ගුණ කළ විට 357ක් ලැබේ. දශම ස්ථාන ගණන 2 නිසා 100න් හෙවත් 10යේ දෙවැනි බලයෙන් ගුණකළ යුතුයි. භාජකය පූර්ණ සංඛ්යා වක් කිරීමට 10යේ බලයකින් ගුණ කරනවා නම් භාජ්යය ද එම දහයේ බලයෙන් ම ගුණකළ යුතුයි. එම නිසා මේ අන්දමට භාජකය ද භාජ්යය ද වෙනස් කර බෙදීම කළ හැකිය. දශම භාගයකින් බෙදීම තවත් අන්දමකට කළ හැකිය. භාජ්යයේ ද භාජකකයේ ද දශම තිත් නොසලකා බෙදීම කර අවසානයේ දී ලබ්ධියේ දශම තිත තැබීම දළ උත්තරයක් ලබාගැනීමෙන් කළ හැකිය. (දශම භාග බ.)
සාමාන්ය භාග සියල්ල ම දශම භාග හැටියට ලිවිය හැකිය. ලවය හරයෙන් බෙදීමෙන් භාගයට සමාන දශම භාගය සොයා ගත හැකිය. සමහර විට ලැබෙන දශම භාගයේ එක ම අංක පිළිවෙළට ආවර්ත වෙමින් ලැබෙන බව පෙනෙනවා ඇත. එසේ වන විට බෙදීම නවත්වා ආවර්ත වන අංකවලින් පළමු වැනි අංකයේ ද අනිත්ම අංකයේ ද උඩින් තිත් තැබීමෙන් ඒවා දැක්විය යුතුය. උදා. දශම භාගයක් කරන විට 027 ආවර්ත වෙමින් ලැබෙන බව පෙනේ. මෙය ලියන්නේ මෙසේය.
= .027027 = .027
මෙවැනි දශම භාගවලට ආවර්ත දශම භාගයයි කියනු ලැබේ. (ආවර්ත දශමය බ.)
අපරිමේය සංඛ්යා:
2 x 2 = 4; 3 x 3 = 9; මෙය සලකා බලමු. 2ට හතරේ වර්ගමූල යැයි යයි කියනු ලැබේ. 3, 9යේ වර්ගමූලය වේ. මෙසේ 4ට ද 9ට වර්ගමූල තිබේ. 4 ද 9 ද වර්ග පූර්ණ සංඛ්යාවකින් ප්රකාශ හැකි නමුත් 2, 3, 5, 7, 8 ආදි සංඛ්යාවක වර්ගමූල පූර්ණ සංඛ්යාවකින්හෝ සාමාන්ය භාගයකින් හෝ දශම භාගයකින් හෝ නිවරදිව ප්රකාශ කළ නොහැකිය.
2කේ වර්ගමූලය ලියන්නේ මෙසේය: .2කේ වර්ගමූලය ඉතා ආසන්න වශයෙන් සෙවිය හැකිය. දෙකේ වර්ගමූලය 1ටත් 2ටත් අතර සංඛ්යාවක් වන නමුත් එය නිවැරදිව මෙපමණ යැයි කිව නොහැකි බවත් ඍජුකෝණි ත්රිකෝණයක පාද දෙක අඟල් 1 බැගින් දිග නම් එහි කර්ණයේ දිග අඟල් බවත් අවුරුදු 2500කටත් පෙර සිටි පෛතගොරස් නමැති පණ්ඩිතයා පෙන්වා දුන්නේ ය. මේ ත්රිකෝණයේ කර්ණය අඟල් ට සමාන සරල රේඛාවක් වේ. නමුත් එහි දිග කොපමණ දැයි දශම භාගවලින් හෝ සාමාන්ය භාගවලින් නිවැරදිව මැනිය නොහැක.
වැනි සංඛ්යාවන්ට අපරිමේය සංඛ්යා යයි කියනු ලැබේ. අපරිමේය සංඛ්යා යනු දශම භාග සාමාන්ය භාගවලින් නිවැරදිව ප්රකාශ කළ නොහැකි සංඛ්යායි. දර්ශකය අනුව අපරිමේය සංඛ්යා ද ගණිත කර්මවලට යෙදිය හැකිය. පළමුවෙන්ම විස්තර කරන ලද දර්ශක නිතිවල දී දර්ශක පූර්ණ සංඛ්යා හැටියට සලකා ඇත.
නමුත් එම නිතිවල දර්ශක මොනවා වුවත් ඒ නිති සැබෑ බව පිළිගත් විට, සංඛ්යාවක බලයක් මෙන් පෙන්විය හැක.
2 කේ වර්ගමූලය 2 කේ n බලය යයි සලකමු.
2n x 2n = 2
22n = 2
2n = 21/2
n = ½
= 21/2
මේ අන්දමට භාග දර්ශක යොදා අපරිමේය සංඛ්යා වල ලක්ෂණ සෙවිය හැක.
පුර්ණ සංඛ්යා යන්නය වඩා නිවැරදි නම ධන පූර්ණ සංඛ්යා බව කලින් කියා ඇත. බින්දුවට අඩු සංඛ්යා තිබිය හැකි බව පැහැදිලි කරුණකි. පූර්ණ සංඛ්යාවකින් 1 බැගින් අඩු කරගෙන යන විට අවසානයේ දී 3, 2, 1, 0 වශයෙන් ලැබේ. බින්දුවට එකක් අඩු සංඛ්යාව 0 – 1 එනම් - 1 වේ. මෙයට සෘණ එක යයි කියනු ලැබේ. ඊට එකක් අඩු සංඛ්යාව - 2 වේ. සෘණ සංඛ්යා මගින් දර්ශක වාදය තවත් පුළුල් කොට ගත හැකිය.
33 = 27
32 = 9
31 = 3 මෙහි දෙපැත්තේ ම සංඛ්යාවන් තුනෙන් බෙදීමෙන් 30 = 1 දර්ශක වාදය අනුව මේ සත්ය අපට ලැබේ. 3 - 1 = 1/3
3 – 2 = 32
දර්ශකය 0 නම්, බලයේ වටිනාකම 1ය. දැන් දශම භාග සංඛ්යාවකින් මෙසේ ප්රකාශනයක් හැටියට ලිවිය හැකිය:-
612.374 = 6 x 102 + 101 + 2 x 100 + 3 x 10-1 + 7 x 10-2 + 4 x 10-3 මෙහි සියලු ම අංක 10 බලයකින් ගුණකර තිබේ.
ලඝුගණක:
ගුණ කිරීමක ද, බෙදීමක ද දශම ස්ථාන ගණනකය නිවැරදි උත්තරයක් දර්ශකවාදයෙහි ප්රතිඵලයක් වන ලඝුගණක මාර්ගයෙන් ලබාගැනීම පහසුය. සංඛ්යාවක් 10 යේ බලයක් හැටියට ප්රකාශ කරන විට, එහි දර්ශකය එම සංඛ්යාවේ ලඝුගණකය වේ.
උදා. 102 = 100. 100යේ ලඝුගණකය (10 පාදයට) = 2
ලඝු 10 100 =2
ලඝුගණක චක්ර මගින් සංඛ්යා දෙකක ලඝුගණකය සොයා ගත් විට සාධක දෙකක් ගුණකිරීම එකතු කිරීමක් වේ. බෙදීම අඩුකිරීමක් වේ.
උදා: ලඝු a = m ; a = 10m
ලඝු b = m; b = 10n
a x b = 10m x 10m = 10m+n
දැන් m + n ලඝුගණකය වූ සංඛ්යාව චක්රයෙන් සොයාගෙන a x b ගුණිතය ලබාගත හැකිය. (එකතු කිරීමට ද අඩු කිරීමට ද පුදුම යන්ත්ර අද මනුෂ්යයා සොයා ගෙන තිබේ. පැරණි කාලයේ පාව්චිචි කළ ගණිත චතුරස්රය එකතු කිරීමට පාව්චිචි කළ යන්ත්රයකි. සර්පණ රූල අද පාවිච්චි කරන සාමාන්ය උපකරණයකි.)
සංඛ්යා:
මෙහි විස්තර කර තිබෙන සංඛ්යා සාමාන්ය වශයෙන් පූර්ණ සංඛ්යා, මූල සංඛ්යා සමාන භාග, දශම භාග අපරිමේය සංඛ්යා යන වර්ගවලට ඇතුළත් වේ. මේ සියලු ම සංඛ්යා තාත්වික සංඛ්යා ගණයට අයත් වේ.
1. එකේ වර්ග මුලය වේ. නමුත් - 1කේ වර්ග
මූලය කුමක්ද? එය අපට
මෙසේ ලිවිය හැක;
මේ සංඛ්යාව ඒ සංඛ්යාවෙන් ම ගුණ කළ විට -1 ලැබෙන බව අපට කිව හැකිය. නමුත් එහි වටිනාකම සෙවිය නොහැක. අංක ගණිතයේ දි මේ සංඛ්යාව භාවිත කරනු නොලැබේ. එවැනි සංඛ්යාවලට අතාත්වික සංඛ්යා යයි කියනු ලැබේ. මේ අතාත්වික සංඛ්යාවල ප්රයෝජනය කුමක් දැයි ගණිතය නොදන්නා කෙනෙකුට කල්පනා කළ නොහැකිය. නමුත් ගණිතයේ ද විද්යාවේ ද මෙය විශෙෂයෙන් බලපාන සංඛ්යාවකි.
පූර්ණ සංඛ්යා: පූර්ණ සංඛ්යා කීප වර්ගයකට බෙදිය හැක. 1, 2, 3, 4, 5, 6, 7 ආදි වශයෙන් සීමාවක් නැතිව පූර්ණ සංඛ්යා තිබේ. පූර්ණ සංඛ්යා ගණන අනන්තය. පුර්ණ සංඛ්යාවන් සාධක සංඛ්යා මූල සංඛ්යා යන කොටස් දෙකට බෙදා ඇත. මූල සංඛ්යාවල ගණන ද අනන්තය. මෙය යුක්ලිඩ් විසින් පෙන්වා දෙන ලදි. සංඛ්යා වාදය මූල සංඛ්යාවල ලක්ෂණ පෙන්වා දෙයි. නමුත් සාමාන්ය මනුෂ්යන් දැනගත යුතු පූර්ණ සංඛ්යා වර්ග කිපයක් තිබේ. 1, 3, 5, 7 ආදි ලැබෙන සංඛ්යාවලට ඔත්තේ යයි කියනු ලැබේ. පළමුවෙනි ඔත්තේ සංඛ්යා දෙක එකතු කළ විට 4 ද තුන එකතු කළ විට 9 ද හතර එකතු කළ විට 16 ද ආදි වශයෙන් ලැබේ.
ඔත්තේ සංඛ්යා: 1, 3, 5, 7, 9, 11, 13
වර්ග සංඛ්යා: 1, 4, 9, 16, 25, 36, 49
මෙසේ 1න් පටන් ගන්නා ඔත්තේ සංඛ්යා ගණනක ඓක්යය එම ගණයේ වර්ගය බව පෙනේ.
උදා. මුල් ඔත්තේ සංඛ්යා 15හේ ඓක්යය 152 වේ. 2, 4, 6, 8, 10 ආදි 2 බැගින් එකතු කර ලැබෙන සංඛ්යාවලට "ඉරට්ට" හෙවත්ත "ඉරත්ත" සංඛ්යා යයි කියනු ලැබේ. ඔත්තේ සංඛ්යා ද ඉරට්ටේ සංඛ්යා ද පූර්ණ සංඛ්යා ද එකට එකක් අනුරූප වන අන්දමට මෙසේ ලියන්න.
1, 3, 5, 7, 9, 11, 13, 15, 17, 19
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
1, 2, 3, 4, 5, 6, 7, 8, 9
මේ පේළි දෙස බලන විට ඉරට්ට සංඛ්යාවක් ඊට අනුරූප ඔත්තේ සංඛ්යාවට එකක් වැඩි බව පෙනේ; එසේ ම ඊට අනුරූප පූර්ණ සංඛ්යාව මෙන් දෙගුණයක් වේ.
5ට අනුරූප ඉරට්ටෙට් සංඛ්යාව 6ය. පූර්ණ සංඛ්යාව 3ය.
6ට වඩා 5 එකකින් අඩුය. 6 = දෙවරක් 3 ව. මුල් ඔත්තේ සංඛ්යා හතේ ඓක්යය 7 x 7 වේ. මුල් ඉරට්ට සංඛ්යා හතේ ඓක්ය 7 x 7 + 7 වේ. එනම් 7 x 8 ය.
මෙසේ පළමුවැනි ඉරට්ටේ සංඛ්යා ගණනක ඓක්යය ඒ ගණන ඊළඟ සංඛ්යාවෙන් ගුණ කිරීමෙන් ලැබේ. පළමුවන පූර්ණ සංඛ්යා 7හි ඓක්යය මෙයින් ½ කි.
පළමුවන පුර්ණ සංඛ්යා 7හි ඓක්යය මෙයින් ඉරට්ට සංඛ්යා ද ඔත්තේ සංඛ්යා ද පූර්ණ සංඛ්යා ද එකතු කිරීමට මේ සුත්ර 3 ලැබේ.
පළමුවැනි ඔත්තේ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය n x n වේ.
පළමුවැනි ඉරට්ට සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය n (n + 1) වේ.
පළමුවැනි පූර්ණ සංඛ්යා ගණන n නම් ඒවායේ ඓක්යය වේ.
එකේ සිට අනුගාමි සංඛ්යා ආකලන වශයෙන් එකතු කළ විට ලැබෙන ඓක්යය ශ්රේණීයට ත්රිකෝණ සංඛ්යා යයි කියනු ලැබේ.
මෙසේ නම් කර තිබෙන්නේ මේවා ත්රිකෝණාකාරයට පිළියෙල කළ හැකි නිසාය.
පුර්ණ සංඛ්යා : 1, 2, 3, 4, 5, 6, 7, 8
ත්රිකෝණ සංඛ්යා : 1, 3, 6, 10, 15, 21, 28, 36
වර්ග සංඛ්යා : 1, 4, 9, 16, 25, 36, 49, 64
එක ළඟ තිබෙන ත්රිකෝණ සංඛ්යා දෙකක් එකතු කිරීමෙන් වර්ග සංඛ්යා (Perfect number): 6හි එම සංඛ්යාව ම හැර අනික් සාධක 1, 2, 3 වේ. ඒවා එකතු කිරීමෙන් 6 ලැබේ.
අංගසම සංඛ්යා (Perfect numbers): 6හි එම සංඛ්යාව ම හැර අනික් සාධක 1, 2, 3 වේ. ඒවා එකතු කිරීමෙන් 628 ලැබේ.
28හි 28 හැර අනික් සාධක 1, 2, 4, 7, 14 වේ. ඒවා එකතු කිරීමෙන් 28 ලැබේ.
6, 28 ආදි මෙවැනි සංඛ්යාවලට අංගසම සංඛ්යා යයි කියනු ලැබේ.
496 ද 8128 ද වෙනත් මෙවැනි සංඛ්යා දෙකක් වේ.
මිත්ර සංඛ්යා: 220හි එම සංඛ්යාව හැර එහි අනික් සාධක එකතු කළ විට 284 ලැබේ. 284 එම සංඛ්යාව හැර අනික් සාධක එකතු කළ විට 220 ලැබේ. මෙවැනි සංඛ්යාවලට මිත්ර සංඛ්යා යයි කියනු ලැබේ.
දශම ක්රමයේ සංඛ්යාවලට තිබෙන ලක්ෂණ කිපයක් පහත දැක්වේ.
I දශම ක්රමයේ සංඛ්යා අතුරෙන් 9 ඉතාමත් පුදුම ලක්ෂණ තිබෙන සංඛ්යාවකි.
9 එකතු කිරීම ද, අඩු කිරීම ද පහසුය. 9 එකතු කිරීම අනික් සංඛ්යාවේ එකස්ථාන අංකයෙන් එකක් අඩුකර දශස්ථාන අංකයට එකක් එකතු කිරීමට සමානය:
8 + 9 = 17 (8 හි දශමස්ථාන අංකය 0 ය.)
17 + 9 = 26
සංඛ්යාවකින් 9ක් අඩුකිරීම ඒකස්ථාන අංකයට 1ක් එකතු කර දශස්ථාන අංකයෙන් 1ක් අඩු කිරීමට සමානය:
25 – 9 = 16
II. දහයට අඩු පූර්ණ සංඛ්යාවක් 9 න් ගුණ කළ විට දක්නා ලද ලක්ෂණ අනුව අංක 2ක් තිබෙන සංඛ්යාවක් 99න් ගුණ කිරීම කළ හැකි ද කියා සෙවීම වටී.
76 x 99 = 7524 76 – 1 = 75
75ත්, 24ත් 99 යි.
මෙයත් සැබෑ බව පෙනේ.
365 x 999 = 364635; මෙසේ ම 9999 න් අංක 4ක් තිබෙන සංඛ්යාවක් ද ගුණ කළ හැකිය.
අංක 2ක් තිබෙන සංඛ්යාවක් ද මේ ක්රමයට 999න් ගුණ කළ හැකිය. සංඛ්යාවක අංක ගණන වමෙන් බින්දු ලියා වැඩි කළ හැකිය. 85 = 085 දැන් අංක තුනක් තිබේ.
85 x 999 = 085 x 999 = 084915
එසේ ම 78 x 9999 = 00779922 = 779922
III. 1089 x 9 = 9801. ගුණ්යෙය අංක පරිවර්තනය කිරීමෙන් මෙය ලැබේ. 10989 x 9 = 98901. මේ ගුණිතය ද එසේ ම ගුණ්යයේ අංක පරිවර්තනය කිරීමෙන් ලැබේ. 1089 හි 0 ටත් 8 ටත් අතරේ 9 ඒවා කොපමණ ලියා බැලුවත් මෙය සත්යයක් බව පෙනේ. 109989 x 9 = 989901
10989 2 = 21978
10989 2 = 87912
මේ ගුණිත දෙකින් එක ගුණිතයක් පරිවර්තනය කිරීමෙන් අනික ලැබේ. 3න් 7න් ගුණ කළත් 4න් 6න් ගුණ කළත් මෙවැනි ප්රතිඵල ම ලැබේ.
IV. 12345679 අපූරු සංඛ්යාවකි. මෙය 9යේ (90ට අඩු) ගුණාකාරයකින් ගුණකළොත් ගුණිතයේ එක ම අංකය ම ලැබේ.
V. සංඛ්යා දෙකක දහයේ ඒවා ගණන සමාන නම්, එකස්ථාන අංක දෙක එකතු කළ විට 10 වේ. නම්, ඒ දෙක ගුණ කිරීම පහසුය.
87 83 = 7221 8 9 = 72 7 3 = 21
95 95 = 9025 9 10 = 90 5 5 = 25
116 114 = 13224 11 12 = 132 6 4 = 24
VI. සියස්ථාන අංකය එකස්ථාන අංකයට සම නොවූ අංක 3 ක් තිබෙන සංඛ්යාවක් ලියන්න. එහි අංක පරිවර්තනය කර ලැබෙන සංඛ්යාව පළමු සංඛ්යාවට වඩා වැඩි නම් ඊට උඩින් ද අඩු නම් ඊට යටින් ද ලියා අඩු කරන්න.
උදා. 563
-365
198 අන්තරයේ අංක ද පරිවර්තනය ද අන්තරයට
+ 891 යටින් ලියා එකතු කරන්න.
1089
පටන ගත සංඛ්යාව කුමක් වුවත් උත්තරය හැම විට ම 1089 වේ.
VII. 8126 11න් ගුණ කරන්න. නැවත එම සංඛ්යාවේ අංක පරිවර්තනය කර 11න් ගුණ කරන්න. ගුණික දෙකේ අංක පරිවර්තනය වී ඇත.
8126 11 = 89386
6218 11 = 68398
පළමුවැනි ගුණිතය පරිවර්තනය කිරිමෙන් දෙවැනි ගුණිතය ලැබේ. සංඛ්යාවක එක ළඟ තිබෙන අංක දෙකක ඓක්යය 10ට අඩු නම්, අංක කීයක් සංඛ්යාවේ තිබුණත් මේ ප්රතිඵලය හැම අවස්ථාවක දී ම ලැබෙනවා ඇත.
. 2 ද පුදුම ලක්ෂණ තිබෙන සංඛ්යාවකි. 1 + 2 + 3 + 4 + 8 + 16 + 32 ආදි වශයෙන් දෙකෙන් ගුණ කර ලැබෙන සංඛ්යා ලිවීමෙන් සංඛ්යා දෙකේ ඓක්යය තුන්වැනි සංඛ්යාවට එකක් අඩුය. පළමුවැනි සංඛ්යා තුනේ ඓක්යය සතරවැන්නට එකක් අඩුය. මේ ක්රමයට මේ සංඛ්යා එකතු කළ හැකිය.
මැජික්ප කොටු: කුඩා හතරැස් කොටු 9ක් තිබෙන හතරැස් කොටුවක අනුගාමි සංඛ්යා 9ක් හරස් අතට ද සිරස් අතට ද කොනින් කොනට ද එනම් විකර්ණයක් දිගේ ද එකතු කළ විට ඓක්යය සම වන සේ ලිවිය හැකිය. 1 සිට 9 දක්වා තිබෙන අනුගාමි සංඛ්යා මේ කොටුවේ මෙසේ ලියා තිබේ.
8 1 6
3 5 7
4 9 2
මෙවැනි කොටුවලට මැජික් කොටු යයි කියනු ලැබේ.
එසේ ම අනුගාමි සංඛ්යා 16ක්, 25ක් 36ක් 49ක් ආදි වශයෙන් මෙසේ මැජික් කොටුවල ලිවිය හැකි
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
මේ මැජික් කොටු ගැන භාරත දේශියයන් අවුරුදු දෙදහකට පෙර දැන ගෙන සිටි බවට සාක්ෂ්ය තිබේ. පළමු අංක 16 පුදුම විදිහට ලියා තිබෙන මැජික් සමචතුරස්රයක් ඉන්දියාවේ ග්වාලියෝර් නගරයේ කොටුවට ඇතුළුවන ස්ථානයේ කුලුනක කපා තිබේ. එම මැජික් කොටුව මෙහි දැක්වේ.:-
15 10 3 6
4 5 16 9
14 11 2 7
1 8 13 12
මෙහි හරහට හා පහළට පමණක් නොව සියලු ම විකර්ණ දිගේ තිබෙන සංඛ්යා ද එකතු කළ විට 34 ලැබේ.
එපමණක් නොව මෙහි තිබෙන සියලු ම සම චතුරස්රවල කොන්වල තිබෙන කොටු හතරේ සංඛ්යා එකතු කළ විට ද 34 ලැබේ.
කර්තෘ:පී. ද ඇස්. කුලරත්න
(සංස්කරණය:1963)