අවලම්බය
පැද්දෙන බට්ටා A ලක්ෂ්යයේ සිට B තෙක්ද ආපසු A පසුකර ගෙන C තෙක්ද ගොස් නැවත A කරා කරන ගමනට එක් දෝලනයකැයි කියනු ලැබේ. එක දෝලනයක් අවසාන කිරීමට ගතවන කාලය ආවර්ත (periodic) කාලය නම් වේ. A0B කෝණයට හෝ AOC කෝණයට විස්තාරය (amplitude) යැයි කියති.
විස්තාරය වඩා විශාල නැත්නම් සරල අවලම්බයක ආවර්ත කාලයේ අගය රදා පවතින්නේ අවලම්බයේ දිග උඩයි. දිග වැඩි වන විට ආවර්ත කාලය ද වැඩි වේ. බට්ටාගේ බර හෝ අවලම්බයේ විස්තාරය හෝ වෙනස් වූ විට ආවර්ත කාලය වෙනස්වන්නේ නැත. එහෙත් විස්තාරය පමණට වඩා විශාල වුවහොත් ආවර්ත කාලය විස්තාරය අනුව ද වෙනස් විය හැකියි. අවලම්බයේ විස්තාරය වෙනස් වූ විට ආවර්ත කාලය වෙනස් නොවන බව පළමුවෙන් දැනගත්තේ ගැලිලියෝ (බ.) ය. ඔහු මෙය දැනගත්තේ අහම්බෙනි. දේවස්ථානයක එල්ලෙන පොකුරු පහනක් දෑතට පැද්දෙන ප්රමාණය කුඩා වුවත් මහත් වුවත් එහි දෝලන කාලය එකම බව හේ දුටුවේය.
සරල අවලම්බයේ ආවර්ත කාලය හෙවත් කම්පන කාලය 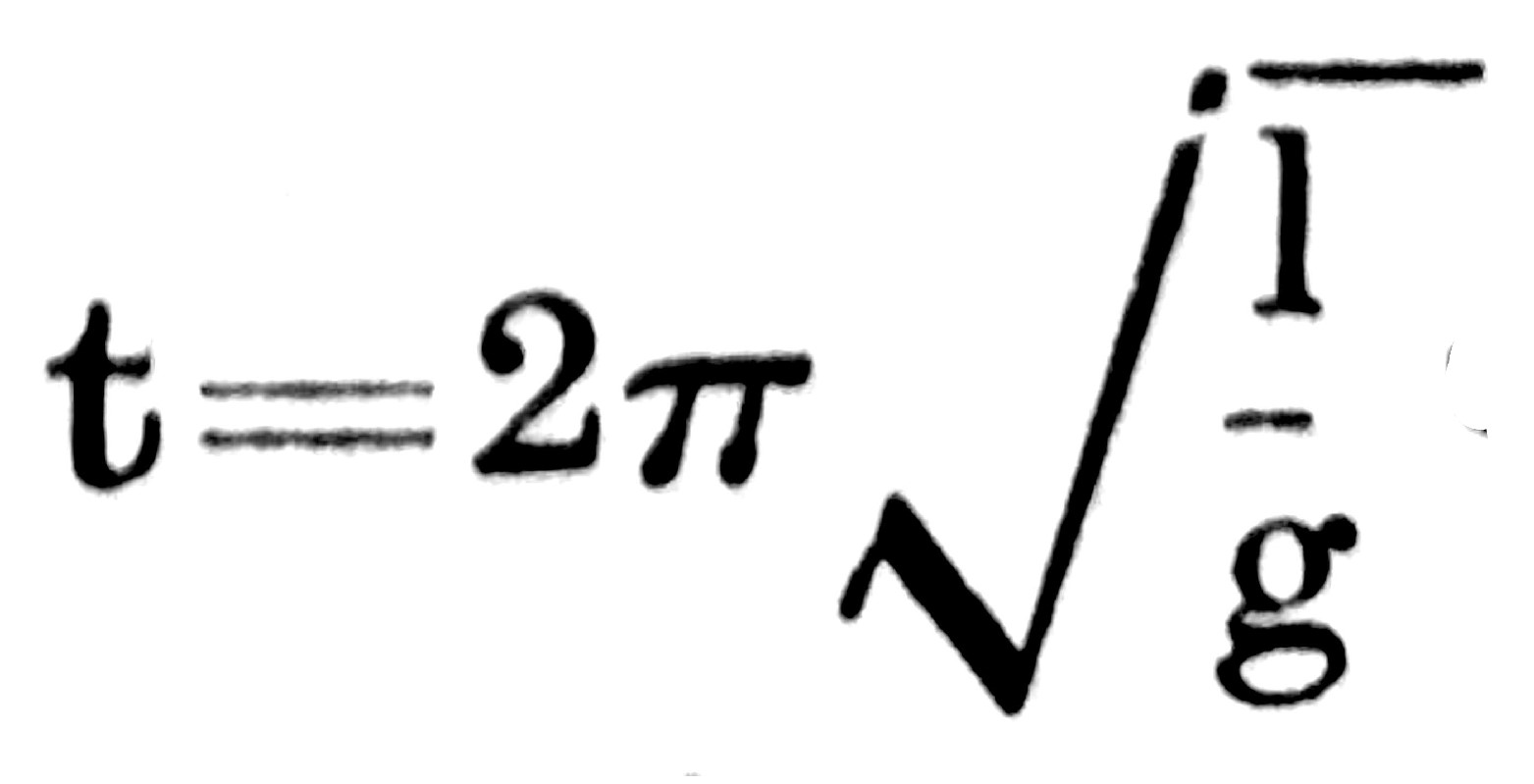 යන සූත්රයෙන් දෙනු ලැබේ. මෙහි t යනු ආවර්ත කාලයයි. I යනු අවලම්බයේ දිගයි. g යනු ගුරුත්වජ ත්වරණයයි. සූත්රයෙහි තිබෙන t සහ I පරීක්ෂණාගාරයෙහි දී මැනීමට පිළිවන් හෙයින් ගුරුත්වජ ත්වරණය සොයා ගැනීමට සරල අවලම්බය වහල් කොට ගත හැකිය. එහෙත් නූල බර නැති දෙයක් නොවන නිසාත් දෝලනය වනු පිණිස ලක්ෂ්යාකාර ස්කන්ධයක් ලබාගත නොහෙන නිසාත් මේ ක්රමය නිවැරැදි නැත. එපමණක් නොව නිශ්චය වශයෙන් ගත හැකි අවලම්බන ලක්ෂ්යයක් ද එයට නැත.
යන සූත්රයෙන් දෙනු ලැබේ. මෙහි t යනු ආවර්ත කාලයයි. I යනු අවලම්බයේ දිගයි. g යනු ගුරුත්වජ ත්වරණයයි. සූත්රයෙහි තිබෙන t සහ I පරීක්ෂණාගාරයෙහි දී මැනීමට පිළිවන් හෙයින් ගුරුත්වජ ත්වරණය සොයා ගැනීමට සරල අවලම්බය වහල් කොට ගත හැකිය. එහෙත් නූල බර නැති දෙයක් නොවන නිසාත් දෝලනය වනු පිණිස ලක්ෂ්යාකාර ස්කන්ධයක් ලබාගත නොහෙන නිසාත් මේ ක්රමය නිවැරැදි නැත. එපමණක් නොව නිශ්චය වශයෙන් ගත හැකි අවලම්බන ලක්ෂ්යයක් ද එයට නැත.
සංයුක්ත අවලම්බය වනාහි තිරස් අක්ෂයක් වටා දෝලනය විය හැකි සේ එල්ලා ඇති දැඩි වස්තුවකි. දණ්ඩ අවලම්බය මෙහි එක් ආකාරයක් වේ.
දැඩි වස්තුවේ ස්කන්ධය M යැයි ද ස්කන්ධ කේන්ද්රයට ඉහළින් r නම් දුරක පිහිටි අක්ෂයක එය පැද්දේ යැයි ද එවිට අක්ෂය වටේට වස්තුවේ අවස්ථිති ඝූර්ණය (moment of inertia) I යැයි ද සිතමු. සංයුක්ත අවලම්බයක ඇතිවන චලිතය නිශ්චය කිරීමේ ගණිත ක්රමය සරල නොවේ. එහෙත් දෝලනයේ විස්තාරය කුඩා නම් චලිතය පිළිබඳ අවකලන සමීකරණයේ (differential equation) (බ.) ඇතැම් පද නොසලකා හැරිය හැකියි. එවිට ලැබෙන සමීකරණය විසඳූ විට අවලම්බයේ දෝලන කාලය ලබා දෙන සමීකරණය ![]() යනු වෙයි.
යනු වෙයි.
යම්කිසි අවමයකට (minimum) වඩා විශාල ඕනෑ ම දෝලන කාලයක් සම්බන්ධයෙන් I⁄r ද එබැවින් t ද සඳහා එකම අගයක් ඇති වෙනස් දුර ප්රමාණ දෙකක් තිබේ. සෛද්ධාන්තික ලෙස ඔප්පු කළ හැකි මෙම කරුණු හොයිගන්ස් (බ.) විසින් පරීක්ෂණාත්මකව සොයා දැන ගන්නා ලදි. මේ දුර ප්රමාණ දෙක ස්කන්ධ කේන්ද්රය (centre of mass) දෙපැත්තෙහි ලකුණු කළවිට එයින් ඇති වන ලක්ෂ්ය දෙකට ප්රතිබද්ධ ලක්ෂ්ය (conjugate points) යැයි කියති. එක් ලක්ෂ්යයකට අවලම්බන කේන්ද්රය යැයි ද අනෙකට දෝලන කේන්ද්රය යැයි ද කියනු ලැබේ. මේ ලක්ෂ්ය අතර ඇති සම්පූර්ණ දුර I යැයි ගත හොත් අවලම්බය එයින් කවර ලක්ෂ්යයකින් එල්ලුව ද පැද්දීමට ගතවන කාලය 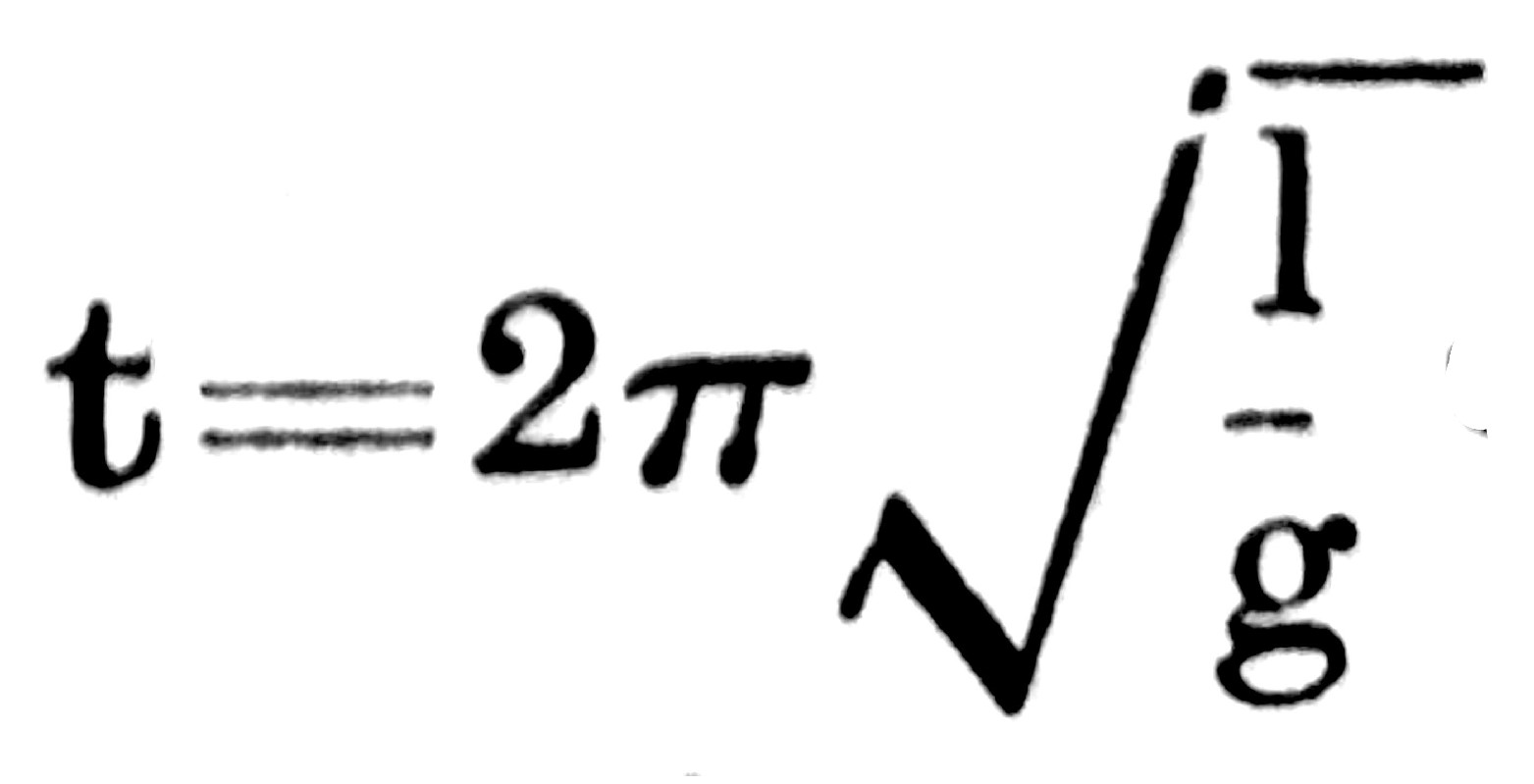 මෙහි I යනු සංයුක්ත අවලම්බයේ දෝලන කාලයට සමාන දෝලන කාලයක් ඇති සරල අවලම්බයක දිග බව පැහැදිලිය. ප්රතිවර්ත්ය (reversible) අවලම්බය සෑදීමේ දී කේටර් විසින් මේ මූලධර්මය ප්රයෝජන කොට ගන්නා ලදි. (රූපය බ.)
මෙහි I යනු සංයුක්ත අවලම්බයේ දෝලන කාලයට සමාන දෝලන කාලයක් ඇති සරල අවලම්බයක දිග බව පැහැදිලිය. ප්රතිවර්ත්ය (reversible) අවලම්බය සෑදීමේ දී කේටර් විසින් මේ මූලධර්මය ප්රයෝජන කොට ගන්නා ලදි. (රූපය බ.)
කාලය මැනීමේ යන්ත්රයක් සෑදීම පිණිස පළමු වරට අවලම්බය උපයෝගි කර ගත්තේ හොයිගන්ස්ය. බට්ටා සහිත ඔරලෝසුව අපට ලැබුණේ ඊට පසුවයි. (ඔරලෝසුව බ.)
(සංස්කරණය: 1965)

