ආලෝකය පිළිබඳ විද්‍යුත්චුම්බක වාදය

ආලෝකය විෂය කොට ඇති අධ්‍යයනය හෙවත් ප්‍රකාශ විද්‍යාව භෞතික විද්‍යාවේ පැරැණිතම ශාඛාවලින් එකකි. අප අසලින් ම ඇති වටපිටාව පිළිබඳව පමණක් නොව අපට සැතැපුම් ලක්ෂ කෝටි සංඛ්‍යාත දුරකින් අවකාශයෙහි පාවෙන ඛගෝල පිළිබඳව ද දැනුම ලබාදීම අතින් ප්‍රමුඛ ස්ථානය ගෙන ඇත්තේ අපගේ පංචේන්ද්‍රියයන් අතුරෙන් දර්ශනේන්ද්‍රිය වන හෙයින් මෙය කිසිසේත් පුදුමයට කරුණක් නොවේ.

ඉතිහාසය

පායන විට ද බසින විට ද මුදුන් වේලාවේ දී පෙනෙනවාට වඩා ලොකුවට ඉර පෙනෙන බව පැරැණි මිසර ලියවිල්ලකින් ශේෂ වී ඇති කොටසක සඳහන් වෙයි. කිරිවාණ විශේෂයකින් සෑදු අභිසරණ කාචයක් (converging lens) නිනෙවායේ නටබුන් අතර තිබී සොයා ගෙන ඇත. ග්‍රීකයන් ඔවුන්ගේ ඉතිහාසයෙහි මුල් හරියේ දී ම දාහකකාච (burning glasses) තනා ගත් බව පෙනේ. ආලෝකය සරල රේඛාකාරයෙන් ගමන් කරන බවත් පරාවර්තනය පිළිබඳ නියමත් ප්ලේටෝගේ දාර්ශනික ගුරුකුලය ඉගැන්වීය. ආලෝකය වර්තනය වන විට වර්තන කෝණය පතන කෝණයට සමානුපාතිකය යන ආවිෂ්කරණය ඇලෙක්සැන්ඩ්රියාවේ විසූ ටොලමි (බ.) නම් නක්ෂත්‍රඥයා ක්‍රි.ව. 139 දී ප්‍රකාශ කෙළේය. කුඩා කෝණ සම්බන්ධයෙන් මෙය බොහෝ දුරට සැබෑය.

ග්‍රීකයෝ, විශේෂයෙන් ම පෛතගෝරස්ගේ හා ඩෙමොක්‍රිටස්ගේ අනුගාමිකයෝ, දෘෂ්ටිය පිළිබඳ සවිස්තර වාද කිහිපයක් ම බිහි කළහ. මේ ගුරුකුල දෙකේ පිළිගැනීම අනුව දෘෂ්ටිය ඇති වන්නේ දීප්ත වස්තුවකින් නිරීක්ෂකයාගේ ඇසට ප්‍රක්ෂිප්ත වන අංශු මගිනි. මේ අදහස මීට සියවස් ගණනකට පසු නිව්ටන්ගේ ආලෝකය පිළිබඳ ලවක වාදයෙහි (ආලෝකය පිළිබඳ ලවක වාදය බ.) ද ඊටත් සියවස් කිහිපයකට පසු ප්ලාන්ක්, අයින්ස්ටයින් යන මොවුන්ගේ ආලෝකය පිළිබඳ ක්වොන්ටම් වාදයෙහි (ආලෝකය පිළිබඳ ක්වොන්ටම් වාදය බ.) ද ගැබ් වී ගියේය.

ගැලීලියෝ විසින් දූරේක්ෂය නිපදවනු ලැබීම හැර ක්‍රිස්තු වර්ෂයෙන් දෙවැනි සියවසේ පටන් දහහත්වැනි ශතවර්ෂය උදාවන තෙක් ආලෝකය නමැති විෂය අතින් කිසි දියුණුවක් වූ බවක් නොපෙනේ. එහෙත් ඩේකාට් (Descartes) (1596–1650), ‍ෆෙර්මා (Fermat) (1601–1665)‚ ග්‍රිමාල්ඩි (Grimaldi) (1613–63), හයිගන්ස් (Huyghens) (1629–1695)‚ හුක් (Hooke) (1635–1703)‚ නිව්ටන් (1642–1727) යන විචක්ෂණ බුද්ධිමතුන් නිසා දහහත්වැනි සියවස තුළ දී ඒ අතින් විශේෂ දියුණුවක් ඇති විය.

ඩේකාට් යන නම බෙහෙවින් ම සිහිපත් කරනුයේ‚ විද්‍යාත්මක කටයුතුවල දී විශ්වය ස්වයංක්‍රිය යන්ත්‍රයක් සේ සැලැකිය හැකි බවත් හැම භෞතික සංසිද්ධියක් සම්බන්ධයෙන් ම යාන්ත්‍රික ආකෘතියක් සිතෙහි මවාගත හැකි විය යුතු බවත් කියැවෙන දර්ශනය බිහි කළ තැනැත්තා වශයෙන්ය. වෙනත් වචනවලින් කියතොත් ඔහුගේ මතය අනුව මේ ද්‍රව්‍යමය ලෝකයේ සිදු වන සෑම සිද්ධියක් ම ගණිත මාධ්‍යයෙන් කල්තියා දැනගත හැකිය.

වස්තූන් අතර ඇතිවන ක්‍රියා විශ්වයෙහි පහසුවෙන් ම දැක ගත හැකි සිද්ධීහු වෙත්. එකකට එකක් ස්පර්ශ වී පවත්නා වස්තූන් අතර ඇති වන ක්‍රියාවන් පීඩන‚ බල ආදිය ඇසුරෙන් පහසුවෙන් පැහැදිලි කළ හැකිය. ද්‍රව්‍යමය මාධ්‍යයක් මඟින් එකකින් එකක් වෙන්ව ඇති වස්තූන් අතර පවත්නා අන්‍යෝන්‍ය ක්‍රියා ද පූර්වෝක්ත මතය ම උපචාර කොට ගැනීමෙන් පැහැදිලි කළ හැකි වෙයි. එනම්‚ බල හා පීඩන එක් වස්තුවකින් අනිකක් වෙත මාධ්‍යය මඟින් සම්ප්‍රේෂණය වන බව කිව හැකිය (නි. කාටීසීය කිමිදින්නා). එහෙත් ඉමහත් දුරකින් වෙන්ව ඇති වස්තු‚ කිසිත් නැති රික්ත අවකාශය පමණක් ඒවා අතර තිබිය දීත් එක එකක් කෙරෙහි ක්‍රියා හා ප්‍රතික්‍රියා කරන්නා වූ අවස්ථා ද ප්‍රකටය. සමුද්‍රයේ වඩදිය හා බාදිය චන්ද්‍රයා නිසා ඇති වන බවත් පෘථිවිය කෙරෙහි සූර්යයා එක එල්ලේ බලපාන බවත් අපි දනිමු. "ඈතක සිට සිදු වන මෙම ක්‍රියාව" පැහැදිලි කරනුයේ කෙසේ ද? අද්භූත බලපෑම් ගැන කීම එය පැහැදිලි කිරීම පිණිස ගන්නා කෙටි මඟක් පමණි. යාන්ත්‍රික පදනමක් මත පිහිටා විවිධ සංසිද්ධීන් පැහැදිලි කිරීමට යත්න දැරූ ඩේකාට්හට ඒ මඟ නුරුස්නා එකක් විය. එසේ හෙයින් වස්තුවල පරමාණු අතර වූ අවකාශය ඇතුළු මුළු අවකාශය ම කිසියම් සියුම් වර්ගයක අංශුවලින් සැදි මාධ්‍යයෙකින් පිරී ඇතැයි ද එම මාධ්‍යය ඉහත කී "කාටීසීය කිමිදෙන්නා" කරන්නාක් මෙන් බල සම්ප්‍රේෂණය කිරීමට හා එහි ගිලී ඇති ද්‍රව්‍යමය වස්තු කෙරෙහි බලපෑම් මෙහෙයැවීමට සමත් යැයි ද යන අදහස හෙතෙම ඉදිරිපත් කළේය. මෙම මාධ්‍යයට 'ඊතර්' යන නම යොදන ලදි. මෙම වචනය ආදි ග්‍රීකයන්ගෙන් රෝමවරුන්ට ලැබී පසුව මධ්‍යකාලීන ප්‍රංස හා ඉංග්‍රීසි ලේඛකයන් විසින් භාවිතයට ගන්නා ලද්දකි. එහෙත් එය එකල භාවිත කරන ලද්දේ මීට ඉඳුරා වෙනස් අර්ථයකිනි. එයට යාන්ත්‍රික ගුණ ආරෝපණය කළා වූ ද පදාර්ථයෙන් පිරී ඉතා සුළු පෙදෙස් හැර මුළු අවකාශය පුරා පැතිර පවත්නා එක ම ද්‍රව්‍ය එය ලෙස සැලකුවා වූ ද මුල් ම තැනැත්තා ඩේකාට්ය. ඩේකාට් විසින් මෙසේ හඳුන්වා දෙන ලද ඊතරය‚ ආලෝකය පිළිබඳ වාදවල දියුණුවක් ඇති කිරීම සඳහා පසුව මහත් සේ උපකාරී විය. ආලෝක තරංග ගමන් ගන්නා මාධ්‍යය වශයෙන් පසු කලෙක දී සලකන්නට යෙදුණේ මේ ඊතරයයි. අන් හැම තරංග වර්ගයකට මෙන් ම ආලෝකයට ද ප්‍රචාරණය සඳහා කිසියම් මාධ්‍යයක් අවශ්‍ය හෙයිනි‚ ඒ.

මීළඟට අපගේ අවධානය යොමු වනුයේ රොබට් හුක් කෙරෙහිය. 1667 දී පළ කරන ලද ලිපියෙක වැදගත් සොයා ගැනීම් දෙකක් ගැන හේ සඳහන් කරයි. වීදුරු තහඩු දෙකක් අතර රැඳුණු තුනී වාත පටලයක් මත ආලෝකය පතිත වූ විට දක්නට ලැබෙන දේදුන්න වැනි වර්ණ ඉන් එකෙකි. පාරාන්ධ වස්තුවක සෙවණැල්ල මුළුමනින් ම අඳුරු වූවක් නොව මඳ ප්‍රදීපනයකින් යුත් වූවක් බව දෙවැන්නයි. ආලෝකය ගමන් කරන්නේ සරල රේඛාකාරයෙන් ම නොවන බවත් බාධක හමුවේ ආලෝකයට නැමී යා හැකි බවත් දෙවැන්නෙන් හැඟැවෙයි.

මෙම සොයා ගැනීම් දෙක ආලෝකය පිළිබඳ කිසිදු ලවක වාදයෙකින් පැහැදිලි කළ නොහැකිය. ඒ සඳහා තරංග වාදයක් අවශ්‍යය. හුක්ගේ දෙවැනි නිරීක්ෂණය එසමයෙහි දී ම පාහේ වුව ද ඔහුගෙන් සහායක් නැතිව ම ග්‍රිමාල්ඩි විසින් ද පළ කරන ලදි. එම සංසිද්ධිය 'විවර්තනය' (diffraction) යැයි හේ නම් කෙළේය.

හුක්, නිරීක්ෂකයකු පමණක් නොව සෛද්ධාන්තිකයෙක් ද වීය. ආලෝක ප්‍රචාරණය පිළිබඳ ඔහුගේ සෛද්ධාන්තික අන්වේෂණ සලකා බැලීම වටී. ඔහුගේ අදහස් සැකෙවින් මෙසේයි:

(1) දීප්ත වස්තුවක කොටස් ශීඝ්‍ර කම්පන චලිතයකින් යුක්තය.

(2) මෙම කම්පන අවට අවකාශයේ (ඊතරයේ) නිශ්චිත ප්‍රවේගයෙකින් සම්ප්‍රේෂණය වේ.

(3) ප්‍රචාරණය සිදු වන්නේ සරල රේඛා, එනම් කිරණ, දිගේයි.

(4) ප්‍රචාරණය සැම දිශාවකට ම එක ම ප්‍රවේගයකින් සිදු වේ.

මේ අනුව දීප්ත වස්තුවේ සෑම ස්පන්දනයක් හෙවත් කම්පනයක් ම ක්‍රමයෙන් විශාල වී යන ගෝලයක් ඇති කරයි. මෙසේ සමජාතීය මාධ්‍යයක් හරහා, රළ නඟින්නාක් මෙන් විහිදී යන ගෝලවල සෑම කොටසක් ම කිරණවලට ඍජුකෝණික වෙයි.

කම්පන ප්‍රභවය, ප්‍රචාරණයේ පරිමිත ප්‍රවේගය, තරංග පෙරමුණු වැනි තරංග වාදයෙක ඇතැම් මූලික අංග හුක්ගේ පරිකල්පිතයන් අතර ද වූ බව මෙයින් පෙනී යයි.

ආලෝකය පිළිබඳ වාදයන්ගේ ඉතිහාසයේ මීළඟ වැදගත් පියවර ගන්නා ලද්දේ 1678 දී ක්‍රිස්ටියන් හයිගන්ස් විසිනි. හේග්හි උපත ලත් හේ පැරිසියේ විද්‍යාව පිළිබඳ ප්‍රංස ඇකඩමියේ රැස්වීමක දී ඉතා වැදගත් ලිපියක් ඉදිරිපත් කෙළේය. ආලෝකය පිළිබඳ තරංග වාදයක දළ අදහසක් මීට පෙර හුක් විසින් ඉදිරිපත් කරනු ලැබුව ද එවැනි වාදයක් සම්පුර්ණයෙන් ම පාහේ පැහැදිලි කරලීමට මුලින් ම පරිශ්‍රමයක් දරන ලද්දේ හයිගන්ස් විසිනි. දීප්ත වස්තුවකට අයත් කම්පනය වන අංශුවකින් වරෙක ඇරැඹුණු තරංගය අවකාශයේ ප්‍රචාරණය වන ආකාරය සඳහන් නොවීම හුක්ගේ වාදයේ තුබුණු අඩුපාඩුවයි. හයිගන්ස්, දැන් ඔහුගේ නමින් හැඳින්වෙන මූලධර්මයක් මඟින් මේ අඩුව පිරිමැසීය. හයිගන්ස්ගේ මූලධර්මය යනුවෙන් හැඳින්වෙන මෙය භෞතික විද්‍යාවේ වැදගත් තැනක් උසුලයි. හයිගන්ස් පටන් ගත්තේ පහත දැක්වෙන උපකල්පනයන්ගෙනි:

(1) ආලෝක කැළැඹීම් සම්ප්‍රේෂණය කිරිමට සමත්, මුළු අවකාශයේ ම පැතිරී සිටින ඊතරයෙක පැවැත්ම.

(2) ආලෝක ප්‍රචාරණයේ පරිමිත ප්‍රවේගය.

හුක් විසින් ඉදිරිපත් කරන ලද අදහස් අතර ද මේවා විය. තරංග පෙරමුණු පිළිබඳ හුක්ගේ මතය (4 වැනි උපකල්පනය) ද හේ ප්‍රයෝජනයට ගත්තේය. දැනට හයිගන්ස්ගේ මූලධර්මය යනුවෙන් සඳහන් වන තවත් උපකල්පනයක් හයිගන්ස් මේවාට එකතු කළේය.

ආලෝකය පිළිබඳව හයිගන්ස්ගේ (තරංග) වාදයට පදනම් කොට ගන්නා ලද මූලික මත පහත දැක්වේ:

(1) වස්තුවක් ආලෝකය නිකුත් කරන විට එහි අංශු කම්පනය වෙයි.

(2) පදාර්ථයක පරමාණු අතර වූ අවකාශය ඇතුළු මුළු අවකාශය ම ඊතරය යනුවෙන් හැඳින්වෙන කාල්පනික මාධ්‍යයෙකින් පිරී පවතී.

(3) මේ ඊතරයේ අංශු කම්පනයෙහි සමත් වේ.

(4) දීප්ත වස්තුවක කම්පනය වන අංශු මගින් ඊතරය කෙරෙහි ඇති කෙරෙන සෑම කම්පනයක් ම තරංග ස්වරූපයෙන් මුළු ඊතරය පුරා සෑම දිශාවට ම නියත ප්‍රවේගයකින් ප්‍රචාරණය වේ.

(5) පදාර්ථය පවත්නා විට ප්‍රචාරණ ප්‍රවේගය වෙනස් වෙයි.

(6) මේ කම්පනය නිරීක්ෂකයකුගේ ඇසට වන් කල එහි ප්‍රතිඵලයක් වශයෙන් දෘෂ්ටි විතානයේ අංශු කම්පනය වී දෘෂ්ටි සංවේදනය ඇති කරයි.

(7) ඊතරය කෙරෙහි කම්පනයක් ඇති කිරීමෙන් පසු ඒ කම්පනයත් දීප්ත වස්තුවත් අතර කිසිදු සම්බන්ධයක් නැත. ඉන් පසු අවකාශය තුළ ප්‍රචාරණය ඊතරය සතු වගකීමකි.

හයිගන්ස් සිය මූලධර්මය ඉදිරිපත් කෙළේ මේ අවසන් උපකල්පනය සම්බන්ධයෙනි. එය මීළඟ උපකල්පන දෙක වශයෙන් දැක්වේ.

(8) කැළැඹීමක් (හුක් කී තරංග පෙරමුණක්) අවකාශයේ කිසියම් තැනකට ළඟා වූ කල තරංග පෙරමුණේ පිහිටන ඊතර අංශු කැළඹීමට හේතු වූ මුල් දීප්ත වස්තුවේ අංශු කම්පනය වූ ශීඝ්‍රතාවෙන් ම කම්පනය වන්නට පෙලැඹෙයි. ඊතර මත ඇති කෙරෙන මේ කම්පනවලින් ද්විතීයික තරංග හෙවත් හයිගන්ස් තරංගිකා හට ගනී.

(9) මේ ද්විතීයික තරංගිකාවල සාමූහික ප්‍රයත්නයෙන් නව තරංග පෙරමුණ හටගෙන ඒ සිද්ධිය දිගින් දිගට සිදු වේ.

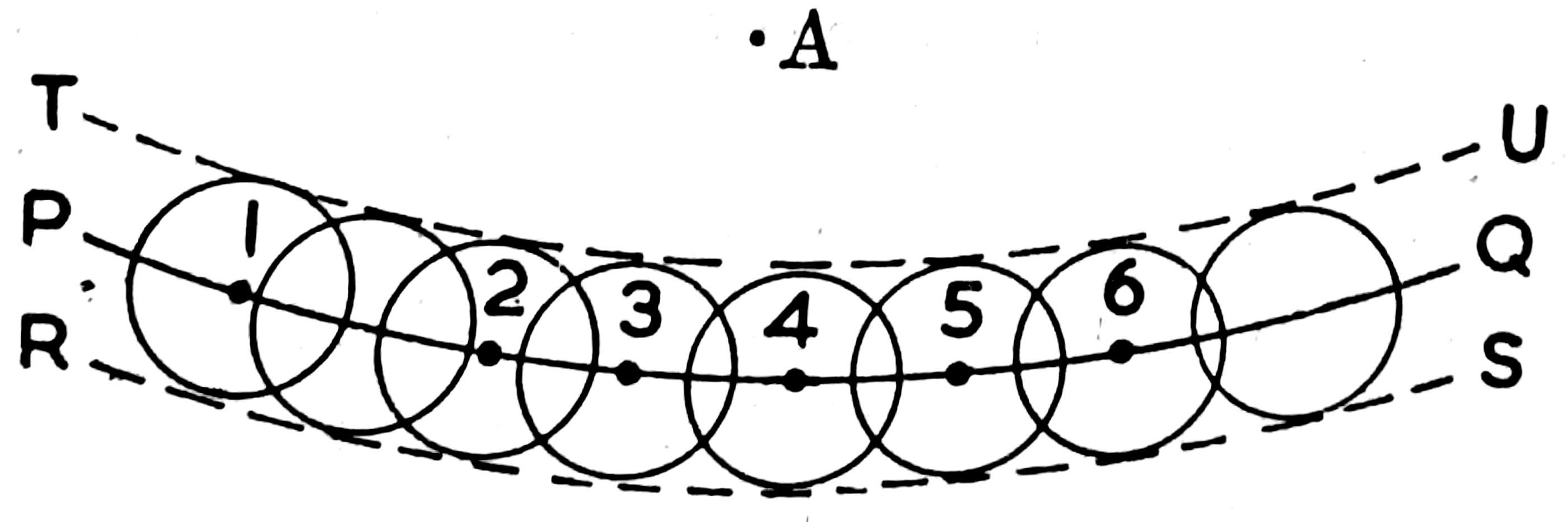
අටවැනි හා නවවැනි උපකල්පන පිළිබඳ පැහැදිලි අවබෝධයක් සරල රූ සටහනක් මඟින් ලබා ගනිමු.

A වූකලි ගෝලීය කැළැඹීම් නිකුත් කරමින් කම්පනය වන්නා වූ ආලෝක ප්‍රභවයකි. PQ යනු ටික වේලාවකට පසු එක්තරා කැළඹීමෙක පිහිටීමයි. 1, 2, 3, 4, .......... යනු ද්විතීයික ප්‍රභවයි, එනම් කැළැඹීම් ගමන් කරන මාර්ගයට යටින් පිහිටි ඊතර අංශුයි. මේවා කම්පනය වන්නට පෙලැඹීම නිසා ගෝලීය කැළැඹීම් හටගනියි. ඒ හයිගන්ස් තරංගිකායි.

මේ කැළැඹීම් RS සහ TU යන වහන්තරා දෙකට මැදි වී පවතී. මේ අනුව හයිගන්ස් තරංගිකා නව තරංග පෙරමුණු දෙකක් - ඉදිරියට ගමන් ගන්නා RS තරංග පෙරමුණත් පස්සට ගමන් ගන්නා TU තරංග පෙරමුණත් - බිහි කරයි. දෙවැන්න පැවැතිය යුත්තක් නොවේ. බොහෝ කලක් යන තෙක් එය තරංග වාදයට විරුද්ධ තර්කයක් ලෙස ඉදිරිපත් කැරිණි. එහෙත් එය නොපවත්නා බව ගණිතානුසාරයෙන් පසු කලෙක පෙන්වා දෙන ලදි. පළමුවැන්න (RS), ප්‍රභවයෙන් නිකුත් වූ සැටියක් පෙන්වමින්, එනම් මුල් කැළඹීමත් හයිගන්ස් කැළඹීමත් එක ම වේගයෙන් ගමන් ගෙන‚ සැලැකිල්ලට ගොදුරු වන අවස්ථාවේ දී TU කැළැඹීම ම ඉදිරියට ගොස් RS පිහිටි තැනට පැමිණි කලක් මෙන් ඉදිරියට ගමන් ගනී.

පරාවර්තනයත් වර්තනයත් පිළිබඳ නියමයන් පැහැදිලි කිරීමට හැකි වී ඇතත් සරලරේඛීය ආලෝක ප්‍රචාරණය පැහැදිලි කිරීමට හයිගන්ස්ගේ තරංග වාදය අපොහොසත් වී ඇත. ජල තරංගත් ධ්වනි තරංගත් මුලු වටා නැමෙන බව ප්‍රකටය. මේ නිසා ආලෝක තරංග පමණක් නොව ඕනෑ ම වර්ගයෙක තරංග මුලු වටා නැමිය යුතු බව කල්පනා කරන ලදි. බොහෝ කලක් යන තෙක් මෙය ආලෝකය පිළිබඳ තරංග වාදයට මහත් බාධකයක් විය. කවර හෙයින්ද යත්, වස්තූන්ගේ ඡායා මූලාකෘතීන්ට අනුරූප බවත් නිශ්චිත බවත් අවධාරණයෙන් පෙන්නුම් කරන ලද හෙයිනි. ආලෝක තරංග මුලු වටා නැමේ නම් එබන්දක් විය නොහේ.

නිව්ටන්ගේ ලවක වාදයත් හයිගන්ස්ගේ තරංග වාදයත් අතර මතභේදය බොහෝ කලක් පැවැතිණි. ආලෝකය නියම සරල රේඛාකාරයෙන් ගමන් නොකරන බව හුක්ගේත් ග්‍රිමාල්ඩිගේ යට සඳහන් නිරීක්ෂණ මඟින් පෙන්නුම් කරන ලද අතර ද්‍රව්‍යමය වස්තු වටා ආලෝකය නැමෙන ප්‍රමාණය තරංග වාදය අනුව ‍ෆ්‍රේනල් (1788–1827) විසින් නිවැරදි ලෙස ගණනය කරන ලදි. හුක් විසින් දක්නා ලද තුනී පටල ඇති කරන වර්ණයන් ලවක වාදයෙන් තේරුම් කළ නොහෙන බවත් ඒ සඳහා කිසියම් තරංග වාදයක් අවශ්‍ය බවත්ය. (1774–1829) කදිම ලෙස පෙන්වා දුන්නේය. මෙසේ ෆ්‍රේනල්ගේත් යංගේත් කටයුතුවලින් ආලෝකය පිළිබඳ ලවක වාදයට මරු පහරක් වැදිණි.

අරාගෝගේ (1786–1853) නිරීක්ෂණයෙක ප්‍රතිඵලයක් වශයෙන් මාලස්ගේ (1775–1812) මේ හා අසම්බන්ධ නොවන නිරීක්ෂණයක් මඟින් ද බාතොලිනස්ගේ (1625–1698) නිරීක්ෂණයෙකින් ද තරංග වාදයට තවත් රුකුල් ලැබිණි. භ්‍රමණය වන නිකල් ප්‍රිස්මයක් (Nicol prism) තුළින් නිල් (වලා නැති) අහස දෙස බැලුවහොත් දක්නට ලැබෙන ආලෝකයේ තීව්‍රතාවේ විචලනයක් වෙයි. පතන ආලෝකයටත් එකිනෙකටත් සම්බන්ධ කොට සුදුසු ලෙස තැබූ දර්පණ දෙකෙකින් පිට පිට ද පරාවර්තනය වීමෙන් ආලෝකය නැති වී යන බව මාලස් දුටුවේය. එක් එක් වීදුරු තහඩුව ආලෝකය පරාවර්තනය කරන අතර දෙක එකට ගත් කල එසේ කරන්නට අපොහොසත්ය. තව ද වීදුරු පුවරුවක් හෝ දියකඳක් හෝ හරහා කිසියම් වස්තුවක් දෙස බැලුවහොත් එක ප්‍රතිබිම්බයක් පමණක් පෙනෙන අතර ආකරලුණු, ක්වෝට්ස් වැනි ස්ඵටිකයන් හරහා බැලුවහොත් ප්‍රතිබිම්බ දෙකක් දක්නට ලැබේ. මේ සංසිද්ධිය පසු කලෙක ද්විත්ව වර්තනය යනුවෙන් හැඳින්විණ. මෙසේ අසම්බන්ධ ස්වාධීන සංසිද්ධි තුනක් වශයෙන් පෙනුණු මේවා එකකට එකක් සම්බන්ධ බවත් ආලෝකයේ එක්තරා ගුණයෙකින් හට ගන්නා බවත් පසුව පෙන්වන ලදි. මේ නිසා ආලෝක ප්‍රචාරණය එහි මාර්ගය වටා සමමිතික නැතැයි නිගමනය කිරීමට සිදු වේ. මේ නයින් ආලෝකය පිළිබඳ විෂයට ධ්‍රැවණය (polarization) නම් නව අංශයක් එක්විණි.

නිව්ටන් අදහස් කළ ලවක හෙවත් ආලෝක අංශු ඉතාමත් කුඩා යැයි ද උල් හැඩයේ යැයි ද සලකනු ලැබේ. එබැවින් ඒවා හොඳින් සමමිතික විය යුතුය; එමෙන්ම ඒවායේ ප්‍රචාරණය කිසි ම අසමමිතියක් තිබිය නොහැකිය. ලවකයෙක මාර්ගයක් හරහා ඇඳි සෑම තලයෙක ම තත්වය ඒකාකාර ම වේ. තරංග පිළිබඳ තතු දැන් සලකා බලමු. අන්වායාම තරංගයැ, තීර්යක් තරංග යැයි තරංග දෙවර්ගයකි. අන්වායාම තරංගවල ප්‍රචාරණයට අදාළ වූ කම්පනය වන අංශු ප්‍රචාරණ දිශාව එල්ලේ කම්පනය වේ. අන්වායාම තරංග පිළිබඳ නිදසුන් නම් වාතයේ ධ්වනි තරංග, දික් අතට පිරිමදින ලද කම්බි පොලු හා කම්බි දිගේ හට ගැනෙන තරංග යනාදියයි. මේ වර්ගයේ කම්පනයේත් ප්‍රචාරණයේත් නියම සමමිතියක් තිබෙන බව පැහැදිලි ය. අනෙක් අතට තිර්යක් තරංගවල කම්පනයෝ ප්‍රචාරණ දිශාවට ලම්බ වෙත්. නිදසුන් නම්, දිය මතුපිට තරංග, වීණාවක තත් පෙළුැ විට එහි හටගන්නා කම්පන යනාදියයි. මේවායේ අංශු කම්පනය වන්නේ කම්පන තලය නමින් දන්නා එක තලයෙකය. එබැවින් අසමමිතියක් හට ගනී. මෙසේ ආලෝකයේ ධ්‍රැවණය පිළිබඳ සංසිද්ධිය වටහා ගැනීමට ආලෝකය පිළිබඳ තරංග වාදය පමණක් නොව ආලෝක තරංග තිර්යක් විය යුතු බව ද අවශ්‍ය කරුණු සේ පිළිගත මනායි. ලවක වාදය මෙයින් සහමුලින් බිඳ වැටී යයි. ආලෝකය හා සම්බන්ධ සංසිද්ධි සියල්ල ම තේරුම් කරලීමට තරංග වාදය සමත් යැයි සැලැකෙන්නට විය. එහෙත් මේ තෘප්තිකර හැඟීම වැඩිකල් නොපැවතියේය. කල් යන්නට පෙර නොසිතූ විරූ විවිධ පැතිවලින් තරංග වාදයේ පදනම් දෙදරැවිණි. ඒ ගැන තොරතුරු මතු සඳහන් වේ. 19 වැනි සියවසේ පසු අඩෙහි දී සෛද්ධාන්තික අතින් ක්ලාක්-මැක්ස්වෙල් (1831-1879) විසින් ද පරීක්ෂණාත්මක කරුණු අතින් හයින්රික් හෙර්ට්ස් (1857-1894) විසින් ද තරංග වාදයට නොයෙක් දෑ එකතු කරන ලදි.

කම්බියෙක ගලන විද්‍යුත් ධාරාවක් ඒ කම්බිය වටා චුම්බක ක්ෂේත්‍රයක් ඇති කරන බව අ’ස්ටෙඩ් (1777-1851) පෙන්වා දෙන තෙක් චුම්බකත්වයත් විද්‍යුතයත් භෞතික විද්‍යාවේ ඉඳුරා ම වෙනස් වූ ස්වාධීන අංශ දෙකක් ලෙස සැලැකිණ. අනතුරුව භෞතික විද්‍යාවේ මෙකී අංශ දෙක විද්‍යුත්චුම්බකත්වය නමින් හැඳින්වෙන එකම අංශයක් බවට පත්විය. මීළඟ පියවර වූයේ මයිකල් ෆැරඩේ (1791–1867) විසින් විද්‍යුත් චුම්බක ප්‍රේරණය සොයා ගනු ලැබීමයි. දඟරයක් හරහා පවතින චුම්බක බලරේඛා ගණන විචලනය වන්නට සැලැසූ කල ධාරාවක් - එහෙයින් විද්‍යුත්ගාමක බලයක් - දඟරයෙහි ප්‍රේරණය වන බව පරීක්ෂණානුසාරයෙන් ෆැරඩේ පෙන්වූයේය. විද්‍යුත් චුම්බකත්වයේ එක්තරා පරස්පරතාවක් මේ නිරීක්ෂණ දෙක මඟින් ප්‍රකාශ වේ.

යථෝක්ත නිරීක්ෂණ දෙකට අදාළ කරුණු ගැඹුරට දැක ගැනීමේ තීක්ෂණ බුද්ධියක් මැක්ස්වෙල්ට තිබිණ. ඔහුගේ තර්කණය මෙසේ විය. අ’ස්ටෙඩ්ගේ සොයාගැනීම අනුව අනවරත විද්‍යුත් ධාරාවක් ඒ අවට අනවරත චුම්බක ක්ෂේත්‍රයක් ඇති කරයි. එබැවින් විචලනය වන ධාරාවක් විචලනය වන චුම්බක ක්ෂේත්‍රයක් ඇති කරන්නේ යැයි බලාපොරොත්තු විය යුතුය. එහෙත් අ’ස්ටෙඩ්ගේ විද්‍යුත් ධාරා ගලා ගියේ කම්බි දිගේය. හිස් අවකාශයේ ගලන ධාරා තිබෙන්නට බැරි දැයි මැක්ස්වෙල් ප්‍රශ්න කළේය. අවකාශයේ ගමන් කරන විද්‍යුත් ආරෝපණ (එනම්, ඉලෙක්ට්‍රෝන) විද්‍යුත් ධාරාවක් වශයෙන් සැලකෙන බවත් එහෙයින් ඒවායින් චුම්බක ක්ෂේත්‍රයක් හටගත යුතු බවත් නොකිවමනායි. අවකාශයේ ඇති මේ වර්ගයේ ධාරා හැරෙන්නට හිස් අවකාශයේ තවත් වර්ගයෙක ධාරා ඇතැයි යන අදහස මැක්ස්වෙල්ට පහළ විය. මේ වර්ගයේ ධාරාවන්ට 'විස්ථාපන ධාරා' යැයි හේ නම් තැබීය. විද්‍යුත් කොන්ඩෙන්සරයෙක අග්‍රවලට විභව අන්තරයක් යෙදූ කල කොන්ඩෙන්සරය තුළ සිදු වන දෑ සලකා බලන්නට මැක්ස්වෙල් කියයි. කොන්ඩෙන්සරය සම්පුර්ණයෙන් ම ආරෝපිත වන තෙක් ම එහි එක් තහඩුවක් ධන විද්‍යුතයෙනුත් අනෙක සෘණ විද්‍යුතයෙනුත් ආරෝපණය වෙයි. ආරෝපණය සිදුවෙද්දී කොන්ඩෙන්සරය විභව ප්‍රභවයෙන් ධාරාවක් ඇද ගන්නා බව පැහැදිලිය. ආරෝපණ පරිපථයේ තැබූ මීටරයෙකින් ඒ බව පෙනී යයි. ආරෝපණ ප්‍රභවයේ සිට සම්බන්ධන කම්බි ඔස්සේ කොන්ඩෙන්සර තහඩුවලට ගලා යන සන්නයන ධාරාව කොන්ඩෙන්සර තහඩු අතර වූ අවකාශය තුළින් ද නොකැඩී යා යුතුය යන අපූරු අදහස මැක්ස්වෙල්ට පහළ විය. අන් අයුරෙකින් පවසතොත්, කම්බි නැති විට පවා ධාරාවේ ගැලීම සන්තත විය යුතු බවට මැක්ස්වෙල් තර්ක කළේය. හිස් අවකාශයේ ගලන මේ ධාරාව 'විස්ථාපන ධාරාව' යනුවෙන් මැක්ස්වෙල් හැඳින්වූයේය.

කොන්ඩෙන්සර තහඩු අතර ඇත්තේ හුදෙක් විද්‍යුත් ක්ෂේත්‍රයකි. පරීක්ෂණයෙන් පෙන්විය හැකි පරිදි කොන්ඩෙන්සර තහඩු මත ඇති ආරෝපණ විචලනය වත් ම මේ විද්‍යුත් ක්ෂේත්‍රය ද විචලනය වෙයි. ගුණන නියතයක් අතින් හැරෙන්නට, විස්ථාපන ධාරාව යනු කාලය අනුව අවකාශයෙහි විද්‍යුත් ක්ෂේත්‍රයේ වෙනස් වීමේ ශීඝ්‍රතාව යන්නම බව සලකා ගැනීමේ අභීත පියවර මැක්ස්වෙල් ගත්තේය. මැක්ස්වෙල්ගේ අදහස අනුව කම්බිවල ගලන සාමාන්‍ය ධාරාවල ගුණත් තත්ත්වයත් විස්ථාපන ධාරාවට තිබිය යුතුය. ඒ අනුව අවකාශයේ විචලනය වන විද්‍යුත් ක්ෂේත්‍රයක් විස්ථාපන ධාරාවන් බිහි කළ යුතුය. එම විස්ථාපන ධාරාවත් කම්බිවල ගලන සාමාන්‍ය ධාරා මෙන් එය වටා චුම්බක ක්ෂේත්‍රයක් ඇති කළ යුතුය. විස්ථාපන ධාරාව කාලය සමඟ විචලනය වෙතොත් එය මඟින් බිහි වුණු චුම්බක ක්ෂේත්‍රය ද කාලය සමඟ විචලනය විය යුතු බව ඊළඟ නිගමනයයි.

මේ ලිපියේ කලින් සඳහන් වුණු විද්‍යුත්චුම්බක ප්‍රේරණය පිළිබඳ ෆැරඩේ නියමය ගැන නැවත මඳක් සලකා බලමු. දඟරයක් හරහා ඇති චුම්බක බල රේඛා ගණන විචලනය වන කල දඟරයේ විද්‍යුත්ගාමක බලයක් ප්‍රේරණය වන බව දුටිමු. දඟරයේ නිදහස් ඉලෙක්ට්‍රෝන, ධාරාවක් සෙයින් දඟරය දිගේ ගලා යන්නට සලස්සන විද්‍යුත් ක්ෂේත්‍රයක් දඟරයේ සෑම ලක්ෂ්‍යයෙක ම හට ගන්නා බව මින් කියැවේ. මැක්ස්වෙල් මේ ප්‍රතිඵලය විශේෂ පරිසරයකට සීමා නොකොට පොදු නිගමනයක් බවට පැමිණ විය. කිසිදු දඟර කම්බියක් නොතිබුණ ද හුදෙක් සංවෘත ජ්‍යාමිතික වක්‍රයක් තිබේ නම්, එසේ ම ඒ වක්‍රය හරහා ඇති චුම්බක ස්‍රාවය විචලනය වන්නේ නම්, චක්‍රයේ සෑම ලක්ෂ්‍යයෙක ම ක්‍රියා කරන විද්‍යුත් ක්ෂේත්‍ර තිබෙන බව හේ ප්‍රකාශ කෙළේය. වක්‍රය හරහා වූ චුම්බක ස්‍රාවය විචලනය වන ශීඝ්‍රතාවෙකින් වෙනස් වන්නේ නම් එමඟින් ඇති වුණු විද්‍යුත්ක්ෂේත්‍රය ද කාලය සමඟ වෙනස් වෙයි. එනම් විචලනය වන විස්ථාපන ධාරාවක් අවකාශයේ හට ගනී.

දැන් වැදගත් ප්‍රතිඵල දෙකක් අපට ලැබී ඇත. ඒ දෙක එක් තැන් කොට ගනිමු.

(1) අනියත ශීඝ්‍රතාවෙකින් විචලනය වන විස්ථාපන ධාරාවක් විචලනය වන චුම්බක ක්ෂේත්‍රයක් අවකාශයේ ඇති කරයි. මෙය වූ කලි අ’ස්ටෙඩ්ගේ සොයා ගැනීමේ විස්තාරණයක් හා සාමාන්‍යකරණයකි.

(2) අනියත ශීඝ්‍රතාවෙකින් විචලනය වන චුම්බක ක්ෂේත්‍රයක් විචලනය වන විස්ථාපන ධාරාවක් ඇති කරයි. මෙය ෆැරඩේගේ සොයා ගැනීමේ විස්තාරණයක් හා සාමාන්‍යකරණයකි.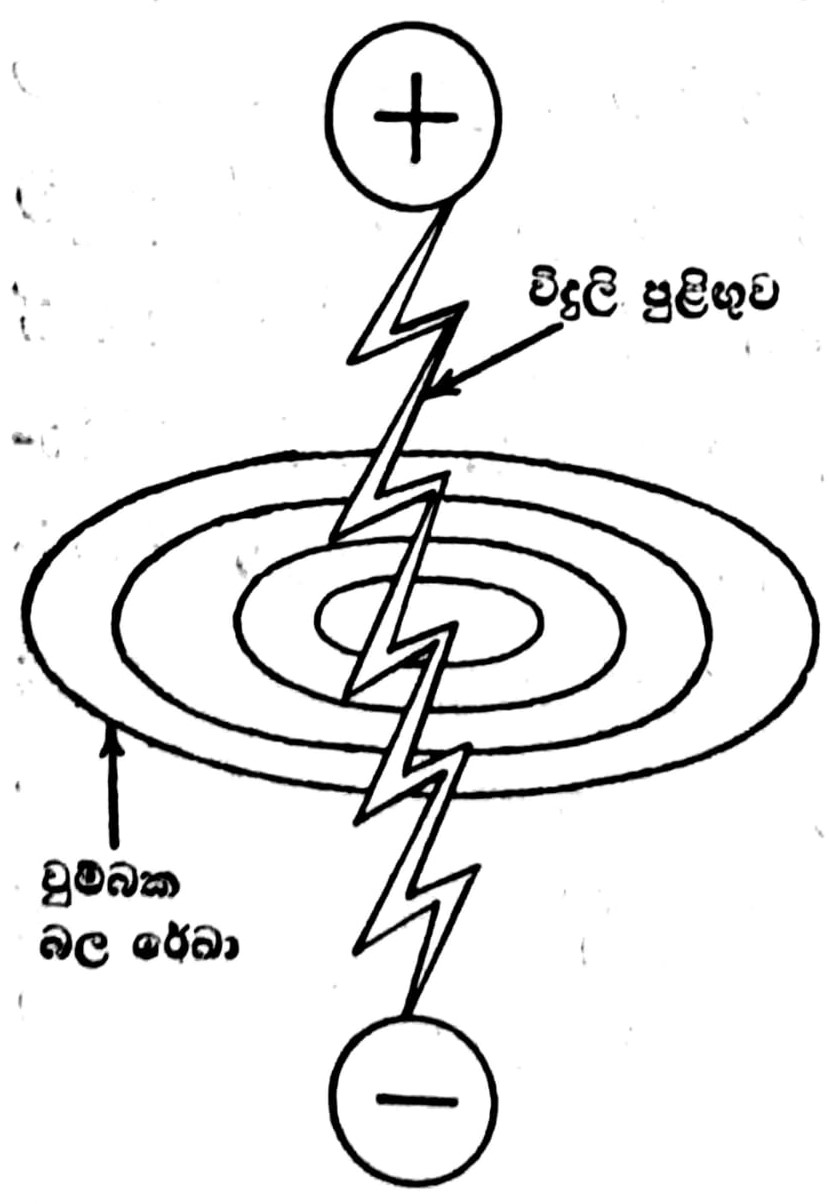

මැක්ස්වෙල්ගේ මේ සාමාන්‍යකරණ දෙකේ ප්‍රතිඵල ගැන සලකා බලමු. ආරෝපිත වස්තු දෙකක් අතර විද්‍යුත් විභව අන්තරය කොපමණ විශාල ද යත්: එකෙකින් අනෙකට විදුලි පුළිඟුවක් ගමන් කරන්නේ යැයි සිතමු. සන්නායක අතර ද විද්‍යුත් ක්ෂේත්‍රය විචලනය වන ශීඝ්‍රතාවෙකින් වෙනස් වෙයි. එබැවින් සන්නායක අතර විස්ථාපන ධාරාවක් ගලයි. එය ද විචලනය වෙයි. (1) අනුව, මේ විස්ථාපන ධාරාව පහත දැක්වෙන පරිදි එය වටා චුම්බක ක්ෂේත්‍රයක් ඇති කරයි.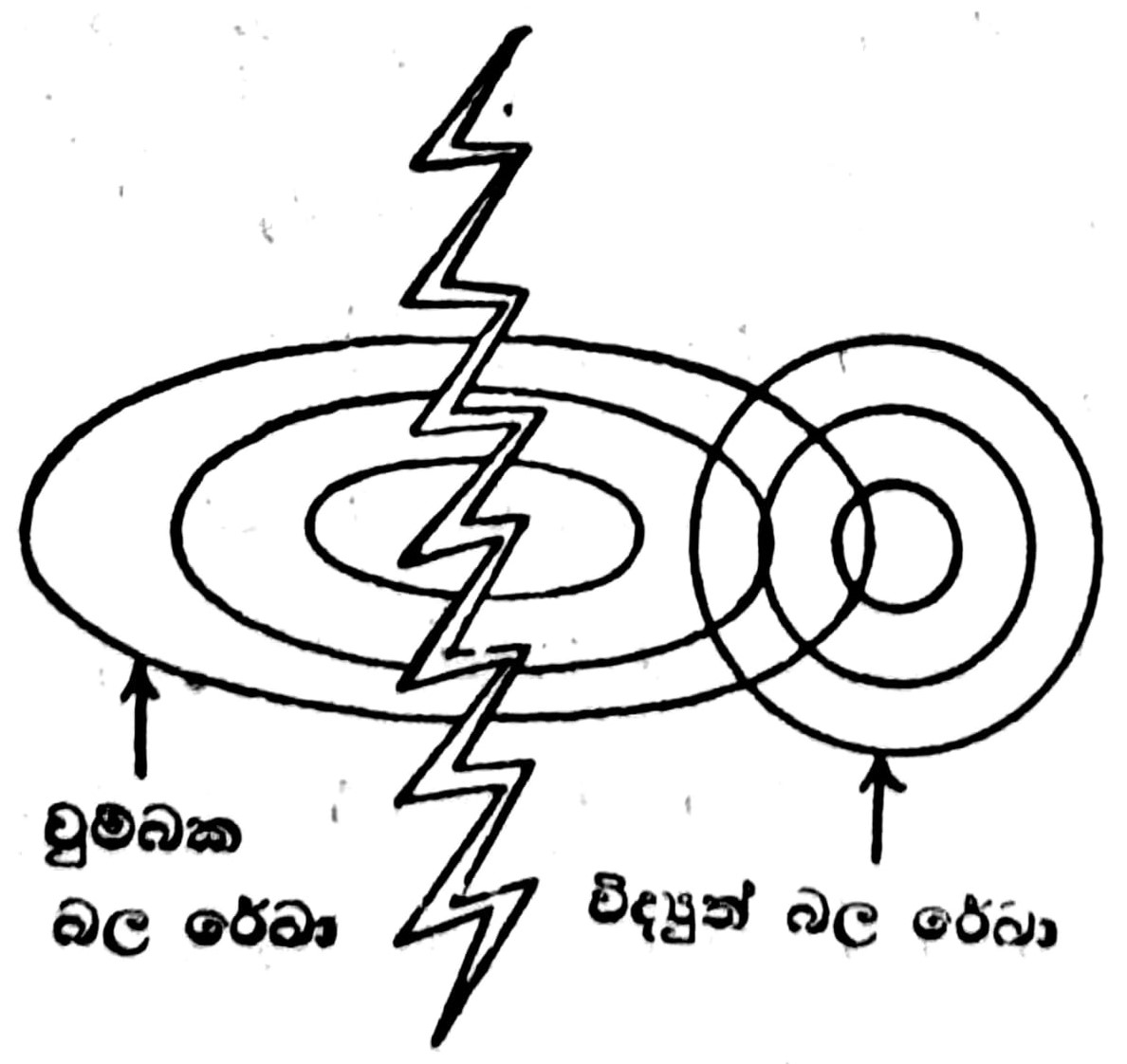

එහෙත් විස්ථාපන ධාරාව කාලයත් සමඟ විචලනය වන බැවින් චුම්බක ක්ෂේත්‍රය ද කාලය සමඟ විචලනය වෙයි. එබැවින් (2) අනුව පහත දැක්වෙන පරිදි චුම්බක බල රේඛා වට කොට විද්‍යුත් බලරේඛා පිහිටයි.

චුම්බක ක්ෂේත්‍රයත් විද්‍යුත් ක්ෂේත්‍රයත් අනියත ශීඝ්‍රතාවකින් විචලනය වන බැවින් එහි ප්‍රතිඵලය ප්‍රචාරණය වන්නේ මෙසේයි:

අන් අයුරෙකින් පවසතොත් අවකාශයේ ප්‍රචාරණය වන විද්‍යුත්චුම්බක තරංගයක් මෙහි දී ඇති වෙයි. මෙහි විද්‍යුත් මුහුණුවරකුත් චුම්බක මුහුණුවරකුත් යනුවෙන් දෙපැත්තක් ඇති බවත් ඒ දෙක ම එක විට ප්‍රචාරණය වන බවත් සැලකිය යුතුය. මේ වර්ගයේ තරංගයක සම්ප්‍රේෂණ ප්‍රවේගය සෛද්ධාන්තික කරුණු ඇසුරෙන් ගණනය කිරීමට මැක්ස්වෙල් සමත් විය. එය ආරෝපණයේ ස්ථිති විද්‍යුත් ඒකකයට ආරෝපණයේ විද්‍යුත් චුම්බක ඒකකය දරන අනුපාතයට සමාන බව පෙනී ගියේය. මේ අනුපාතය මනින ලදුව එය 3X10 10 බව සොයා ගෙන ඇත. එය තත් සෙමීවලින් ගත් කල හිස් අවකාශයේ දී ආලෝකයේ ප්‍රවේගය තරම් වෙයි. මෙය හුදෙක් අහම්බෙන් සිදු වූ සම්පාතයකැයි සැලකෙන්නට ඉඩ තිබිණ. එහෙත් හෙර්ට්ස් විද්‍යුත් චුම්බක තරංගවල ප්‍රවේගය කෙළින්ම මැන, එය ආලෝකයේ ප්‍රවේගය හා සම බව දුටුවේය. එබැවින් ආලෝක තරංගත් විද්‍යුත් චුම්බක තරංගත් අවකාශය තුළ එක ම ප්‍රවේගයෙන් ගමන් කරන හෙයින් එක ම ස්වභාවයේ ඒවාය යන නිගමනයට එළැඹෙන්නට කෙනෙකුට සිදු වේ. එතෙක් එකකට එකක් සම්බන්ධ නොවූ විෂය දෙකක් වශයෙන් සැලැකුණු භෞතික විද්‍යාවේ අංශ දෙකක් වන ආලෝකයත් විද්‍යුතයත් මැක්ස්වෙල් ස්වකීය සාමාන්‍යකරණ දෙක මඟින් එක්කොට ලූයේය.

මැක්ස්වෙල්ගේ විද්‍යුත්චුම්බක වාදය කලින් පැවති හයිගන්ස්ගේත් ෆ්‍රේනල්ගේත් තරංගවාදය හා ගැටුණ ද ආසන්න සරල රේඛීය ආලෝක ප්‍රචාරණය, ආලෝකයේ නිරෝධනය, විවර්තනය හා ධ්‍රැවණය යන මේ කරුණු තේරුම් කරලීමට ඉවහල් වූ යථෝක්ත තරංග වාදයේ අංග කෙරෙහි එය බල නොපෑවේය. හයිගන්ස්ගේත් ‍ෆ්‍රේනල්ගේත් වාදයේ කම්පනය වේ යයි සලකන ලද්දේ ඊතර අංශුයි. එහෙත් මැක්ස්වෙල්ගේ විද්‍යුත් චුම්බකවාදයේ එසේ කම්පනය වේ යයි පවසනු ලබන්නේ විද්‍යුත් හා චුම්බක ක්ෂේත්‍ර හෙවත් විද්‍යුත්චුම්බක ක්ෂේත්‍රයි. එහෙයින් වෙනස්කම් සිදු වී ඇත්තේ මූලික කරුණු සම්බන්ධයෙන් මිස මතු පිට මෙන් දක්නට ලැබෙන අංග පිළිබඳ ව නොවේ.

නිව්ටන්ගේ ආලෝකය පිළිබඳ ලවක වාදය ගැන මුල දී සැකෙවින් සඳහන් කරනු ලැබීය. එය හයිගන්ස්ගේ තරංගවාදය සමඟ සුළු කලක් තරඟ කළ ද (අ) ආසන්න සරලරේඛීය ආලෝක ප්‍රචාරණය (ආ) ආලෝක කදම්බවල නිරෝධනය (ඇ) ආලෝකයේ විවර්තනය යන මේ සිද්ධීන් තේරුම් කරලීමට අසමත් වීමෙන් තරංගවාදයට ඉඩ සලසමින් පසු බැසීමට ඊට සිදු විය. ආලෝකයේ ධ්‍රැවණය එවක දැන ගන්නට ලැබී තිබුණි නම් ඒ සංසිද්ධිය තේරුම් කිරීමට ද ලවක වාදය අපොහොසත් වනු නිසැකයි. නිව්ටන්ගේ මතය අනුව ආලෝක ප්‍රභවයක් ආලෝකය නිකුත් කරන්නේ මූනිස්සම් වැනි ගුලි හෙවත් ලවක ස්වරූපයෙනි. මේවා මිනිස් ඇසේ දෘෂ්ටි විතානය මත පතිත වූ කල දෘෂ්ටි සංවේදනය හට ගනී. මෙම ලවක සරල රේඛාකාරයෙන් ගමන් කරන බව නිව්ටන්ගේ පළමු වැනි නියමයෙන් පෙනේ. දර්පණයක් කෙරෙන් ආලෝකය පරාවර්තනය වීම තේරුම් කරන ලද්දේ මෙම ලවකත් දර්පණයත් අතර සිදුවන ප්‍රත්‍යාස්ථ සංඝට්ටන (elastic collisions) පදනම් කරගෙනයි. වර්තනය තේරුම් කිරීම ඊට වඩා දුෂ්කර කරුණක් විය. මෙහි දී තරමක් පුදුමාකාර වූ කල්පිතයක් ඉදිරිපත් කිරීමට නිව්ටන්ට සිදු විය.

ප්‍රකාශ විද්‍යුත් ආචරණය, ප්‍රතිලෝම ප්‍රකාශ විද්‍යුත් ආචරණය හා කෙම්ටන් ආචරණය වැනි ඇතැම් මූලික ස්වාභාවික සිද්ධීන් අනාවරණය වීමේ හේතුවෙන් මේ සියවස මුල් භාගයේ දී කලක් අමතකව ගොස් තුබූ ලවක වාදය මඳක් වෙනස් මුහුණුවරකින් නැවත ඉදිරිපත් වී ඇත. විද්‍යුත්චුම්බක වාදය පදනම් කරගෙන මේ සංසිද්ධි තේරුම් කරලීම කිසිසේත් නොකළ හැක්කක් ව තිබේ. ඒවා සම්පුර්ණයෙන් තේරුම් කරලීමට නිව්ටන්ගේ ලවක වාදයේ මඟ ගත් නමුත් ඊට වඩා නිශ්චිත වූ ලවක වාදයක් අවශ්‍යය. ප්ලාන්ක් හා අයින්ස්ටයින් විසින් ප්‍රකාශිත ක්වොන්ටම් වාදය නමින් හැඳින්වෙන නව ලවක වාදය සඳහන් කරන්නේ නිව්ටන් ප්‍රකාශ කළාක් මෙන් (අ) ආලෝක ප්‍රභවයක්, වෙන් වශයෙන් පවත්නා ලවක හෙවත් ‍ෆෝටෝන හෙවත් ක්වොන්ටම් ස්වරූපය ගත් දීප්ත ශක්තිය නිකුත් කරන බවත් (ආ) ෆෝටෝනයක රැඳී ඇති ශක්තිය විකරණයේ සංඛ්‍යාතයට සමානුපාතික බවත් (ඇ) අවශෝෂණය හටගන්නා විට ෆෝටෝනයක් මුළුමනින් ම අතුරුදහන් වන බවත්ය. එහෙත් තරංග වාදය මැනැවින් තේරුම් කර ලූ නිරෝධනය වැනි සංසිද්ධි තේරුම් කිරීමට නව ලවක වාදය හෙවත් ක්වොන්ටම් වාදය අපොහොසත්ය. මේ අනුව, එකක් හා අනෙක තරක් කරනු වෙනුවට එකකට නුපුළුවන් දෑ අනෙක සපුරාලමින් එකකට එකක් සහාය වුණු ආලෝක වාද දෙකක් මෙම සියවසේ මුල් භාගයේ දී තිබිණ.

මෙම සියවසේ තෙවැනි සිව්වැනි දශකවල දී සෛද්ධාන්තික භෞතිකඥයන් කළ පර්යේෂණයන් කරණ කොටගෙන හයිසන්බර්ග්ගේ අනිශ්චය සම්බන්ධතාත් (uncertainty relationships) අයින්ස්ටයින්ගේ විශේෂ සාපේක්ෂතාවාදයත් පදනම් කර ගත් ක්වොන්ටම් යාන්ත්‍ර විද්‍යාව නම් නව්‍ය විද්‍යා අංශය බිහි විය. ක්වොන්ටම් යාන්ත්‍ර විද්‍යාව විකිරණය සඳහා යොදන ලද්දේ ප්‍රධාන වශයෙන් ම ‍ෆෙර්මි (Fermi) විසිනි (විකිරණ වාදය බ.).

(කර්තෘ: ඒ.ඩබ්ලිව්. මයිල්වාගනම්)

මැක්ස්වෙල්ගේ විද්‍යුත්චුම්බක වාදය

වීදුරු තුළින් ගිය තල-ධ්‍රැවිත ආලෝක කදම්බයකට සමාන්තර ලෙස ප්‍රබල චුම්බක ක්ෂේත්‍රයක් යෙදූ කල ධ්‍රැවණ තලයේ භ්‍රමණයක් සිදු වන බව 1845 දී ‍ෆැරඩේ සොයා ගත්තේය. ආලෝකය ස්වභාවයෙන් විද්‍යුත්චුම්බක විය හැකි බව මුලින් ම පෙනී ගියේ එවිටය. විද්‍යුත් ක්ෂේත්‍ර ද චුම්බක ක්ෂේත්‍ර ද අවට මාධ්‍යයක පවත්නා ප්‍රත්‍යාබල සමූහයක්ය යන මතය ෆැරඩේ ඒ වන විට ගොඩ නඟා තිබිණ. එතෙක් ප්‍රචලිතව පැවති යාන්න්‍ර විද්‍යාත්මක මතය විද්‍යුත් ආරෝපණ තේරුම් කර ලීමට තැත් කෙළේ උදක් ම ආරෝපණ හා සම්බන්ධ අදහස් ඇසුරෙනි. විද්‍යුත් චුම්බක සංසිද්ධි විස්තර කිරීමේ දී ක්ෂේත්‍රයට වඩාත් වැදගත් තැනක් දීමට නව්‍ය මත පෙලැඹුණේය. විද්‍යුත් චුම්බක ක්ෂේත්‍රය අද මූලික භෞතික සංකල්පයක් බවට පත්ව ඇත. විද්‍යුත්චුම්බක ක්ෂේත්‍රයක් ආලෝක තරංග ගෙන යන මාධ්‍යයත් අතර සම්බන්ධයක් තිබිය හැකි බව මුලින් ම පෙනී ගියේ ෆැරඩේගේ පරීක්ෂණයෙනි.

‍ෆැරඩේගේ අදහස් ප්‍රධාන වශයෙන් ම ගුණාත්මක විය. විද්‍යුත්චුම්බක ක්ෂේත්‍රය පිළිබඳ ගණිතමය වාදය ගොඩනඟන ලද්දේ 1865 දී ක්ලාක් මැක්ස්වෙල් විසිනි. විද්‍යුත්චුම්බක ක්ෂේත්‍රයේ තරංග තිබෙන බව හෙවත් එකට එක් වුණු විද්‍යුත් ක්ෂේත්‍රවලත් චුම්බක ක්ෂේත්‍රවලත් අවකාශයේ හා කාලයේ සරල අනුවර්තී විචලනයක් ඇති බව හේ නිගමනය කළේය. යථෝක්ත වාදයෙන් මේ තරංගවල ඇතැයි කල් තියා ම ප්‍රකාශිත වූ ගුණ, ආලෝක තරංගවල ඉතා ප්‍රකට ගුණවලට බොහෝ සෙයින් සම විය. ඊටත් වඩා අපූරු දැය නම් ඒවායේ ගණනයෙන් ලබා ගත් ප්‍රවේගයත් පරීක්ෂණ මඟින් දැක ගත් ආලෝකයේ ප්‍රවේගයත් පුදුම සහගත තරම් එකකට එකක් ළං වීමයි. ඉක්බිති එච්.ඒ. ලෝරන්ස් ඇතුළු වෙනත් භවතුන්ගේ පරීක්ෂණයන්ගෙන් මේ සමානකම තවත් තහවුරු විය.

මැක්ස්වෙල්ගේ වාදය මුලින් ම පරීක්ෂණාත්මක ලෙස තහවුරු වූයේ 1887 දී ය. විද්‍යුත් දෝලන හටගන්නා ලේඩන් සරාවක් අවට වූ අවකාශයේ මැක්ස්වෙල් අනාවරණය කළ ආකාරයේ විද්‍යුත්චුම්බක විකිරණ පවත්නා බව ජර්මනියේ හයින්රික් හ’ට්ස් විසින් පෙන්වා දෙන ලදි. මේ විකිරණවල ප්‍රචාරණ ප්‍රවේගය ආලෝකයේ ප්‍රචාරණ ප්‍රවේගය ම බව පසුව පෙන්වනු ලැබීය.

ප්‍රමාණයෙන් විවිධ වූ මේ විකිරණ විශාල සංඛ්‍යාවක් හදාරා ඉන් ලත් ප්‍රතිඵල වැඩට යොදා ගෙන ඇත. ඒ සියල්ල ස්වභාවයෙන් විද්‍යුත්චුම්බක වෙයි. ඒවා අතර කිසියම් ගුණාත්මක වෙනසක් වේ නම් එය නිර්ණය වන්නේ හුදෙක් ඒවායේ තරංග ආයාම අතර පවත්නා ප්‍රමාණාත්මක වෙනසිනි. පහත දැක්වෙන්නේ සුපුරුදු විකිරණ කිහිපයෙකි:

තරංග ආයාමය

y (ගැමා) කිරණ: සෙමී. 10 -12 සිට 10 -10

X (එක්ස්) කිරණ සෙමි. 10 -10 සිට 10 -9

පාරජම්බූල කිරණ: සෙමී. 10 -7 සිට 4x10 -5

දෘශ්‍ය ආලෝකය: සෙමී. 4X10 -5 සිට 7.7X10 –5

අධෝරක්ත කිරණ: සෙමී. 7.7×10 -5 සිට 4X10 -1

රේඩියෝ තරංග: සෙමි. 4x10 -1 සිට 3×‍10 –6

විද්‍යුත්චුම්බක ක්ෂේත්‍ර සමීකරණ

විද්‍යුත්චුම්බක ක්ෂේත්‍රය හඳුන්වන්වනු ලබන්නේ E යන විද්‍යුත් තීව්‍රතාවත් D යන විද්‍යුත් ප්‍රේරණයත් H යන චුම්බක තීව්‍රතාවත් B යන චුම්බක ප්‍රේරණයත් i යන ධාරා ඝනත්වයත් යන මේ දෛශික රාශි ඇසුරෙනි. මේ දෛශිකයෝ සාමාන්‍යයෙන් කාලයත් පිහිටීමත් අනුව වෙනස් වෙත්.

මැක්ස්වෙල්ගේ වාදය මේ රාශි අතර පවත්නා මූලික සම්බන්ධන, එනම් පහත දැක්වෙන සුප්‍රසිද්ධ විද්‍යුත්චුම්බක ක්ෂේත්‍ර සමීකරණ, දෙකකට මඟ පාදයි:

යනු මාධ්‍යයේ විද්‍යුත් සන්නායකතාවයි. к එහි පාරවිද්‍යුත් නියතයයි. μ එහි චුම්බක පාරගම්‍යතාවයි. c යනු ආරෝපණයේ ස්ථිති විද්‍යුත් ඒකකයට (ස්.වි.ඒට) විද්‍යුත් චුම්බක ඒකකය (වි.චු.ඒ.) දරන අනුපාතය දක්වන නියතයකි. ඉහත සඳහන් දෛශික රාශි ප්‍රකාශ කරන්නේ ස්ථිති විද්‍යුත් ඒකකවලිනි.

(1) සමීකරණය වූ කලි ඇම්පියර්ගේ පරිපථ සම්බන්ධනය මැක්ස්වෙල් අතින් සාධාරණීභූත වූ අයුරුයි. එය ඇම්පියර්ගේ සම්බන්ධනයෙන් මෙ‌සේ ලබා ගත හැකියි:

= චුම්බක පරිපථය වටා ඒකක චුම්බක ධ්‍රැවයක් ගෙන යෑමේ දී කැරෙන කාර්යය

= චුම්බක පරිපථයේ ධාරාව (ස්.වි.ඒ වලින්)

මෙහි i=ධාරා ඝනත්වය.

එහෙත් H.ds=ꭍ බඹුර H dS .......ස්ටොක් ප්‍රමේයයෙන්.

එබැවින් = බඹුර H ...........(3)

මැක්ස්වෙල්ගේ අදහස අනුව i යන ධාරා ඝනත්වය (අ) සන්නයන ධාරාවක් යැ (ආ) විස්ථාපන ධාරාවක් යැ යන සංචරක දෙකෙකින් සමන්විතයි.

ඒකක ඝනකයෙක ප්‍රතිරෝධය = ඝනකයේ ප්‍රතිවිරුද්ධ මූණත් හරහා ඇති වි.ගා.බට (e.m.f.) සංඛ්‍යාත්මක වශයෙන් E සමානය.

එබැවින් ඒකක වර්ගඵලයට සන්නයන ධාරාව = E.

විස්ථාපන ධාරාව

පාරවිද්‍යුත් ද්‍රව්‍යයෙක ධාරාවක් හෙවත් විස්ථාපන ධාරාවක් තිබිය හැකි බව පළමුවෙන් ම පෙන්වා දෙන ලද්දේ මැක්ස්වෙල් විසිනි. ඔහුගේ අදහස අනුව මාධ්‍යයෙක විද්‍යුත්ප්‍රේරණයේ ඕනෑම වෙනසක් විද්‍යුත් ධාරාවකි. නිදසුනක් නම්, කොන්ඩෙන්සරයක් ආරෝපණය කිරීමේ දී නැති නම් විසර්ජණය කිරීමේ දී තහඩු දෙක වෙතට හෝ ඒ වෙතින් හෝ ධාරාවක් ගලයි. මේ ධාරාව කොන්ඩෙන්සරය තුළ දී සන්තත බව සැලැකිය හැකියි. පාරවිද්‍යුත් ද්‍රව්‍යය තුළ දී එහි අගය විද්‍යුත් ප්‍රේරණය හෙවත් විස්ථාපනය වෙනස් වීමේ ශීඝ්‍රතාවයි. විස්ථාපන ධාරාවෙක චුම්බක ආචරණ සන්නයන ධාරාවෙක චුම්බක ආචරණවලට සමානය.

එවිට විද්‍යුත් ප්‍රේරණය D

ඒකක වර්ගඵලයට විස්ථාපන ධාරාව

එබැවින්

(3) සමිකරණයේ ආදේශ කිරීමෙන්.

මැක්ස්වෙල්ගේ පළමු වැනි සමීකරණය මෙයයි.

(2) සමීකරණය වූකලි විද්‍යුත්චුම්බක ප්‍රේරණය පිළිබඳ ෆැරඩේ නියමයේ විශ්ලේෂක ආකාරයයි. විද්‍යුත්ගාමක බලය යනු පරිපථයක් වටා විද්‍යුත් තීව්‍රතාවේ රේඛීය අනුකලයයි.

එබැවින් ‍ෆැරඩේ නියමය මෙසේ ලිවිය හැකියි:

මැක්ස්වෙල්ගේ දෙවැනි සමීකරණය මෙයයි.

විද්‍යුත්චුම්බක තරංගයක් සඳහා සමීකරණය

=0 වන සමසාර්වදිශ පාරවිද්‍යුත් ද්‍රව්‍ය පිළිබඳව මෙහි දී සලකා බලනු ලැබේ. (1), (2) සමීකරණවල = 0 ලිවීමෙන් පිළිවෙළින්

තවද පරිමා ආරෝපණය නැතැයි උපකල්පනය කිරීමෙන් විද්‍යුත් හා චුම්බක ක්ෂේත්‍රවල සාන්තත්‍යය පිළිබඳ පහත සදහන් සමීකරණ ප්වාසොං සමීකරණයෙන් ලැබේ.

අපසා E = 0.... (5); අපසා H= 0......(6)

දැන් (4), (2) සමීකරණවලින් E හෝ H හෝ ඉවත් කර ලිය හැකිය. H ඉවත් කිරීම සඳහා (2) සමීකරණයේ බඹුර ගනු ලබන අතර (4) සමීකරණය t විෂයයෙන් අවකලනය කරනු ලැබේ.

මේ අනුව: බඹුර බඹුර E = බඹුර

එනම් අනුක්‍රමණ අපසා E- බඹුර

සහ

එනම් බඹුර ................(8)

අපසා E = ) ලියා (7), (8) සමීකරණ අතරින් බඹුර ඉවත් කිරීමෙන් මෙසේ ලැබේ:

..............(9)

(4), (2) සමීකරණවලින් E ඉවත් කිරීමෙන් H සඳහා එවැනි ම වූ පහත සඳහන් සමීකරණය ලබා ගත හැකිය.

.............(10)

භෞතික විද්‍යාවේ නිතර හමු වන තරංග ප්‍රචාරණය පිළිබඳ සමීකරණයට මේ අවකලන සමීකරණ ඉතාමත් ම සමානය. මේ සමීකරණය හා සැසැඳීමෙන් පෙනී යන්නක් නම් විද්‍යුත්චුම්බක ක්ෂේත්‍රයේ ආවර්ත විචලන ට සමාන ප්‍රවේගයෙකින් යුත් තරංග වශයෙන් අවකාශය හරහා ගමන් කරන බවයි.

තල තරංගයෙක ප්‍රචාරණය

තල තරංගය වූ කලි ඊට සම්බන්ධ සියලු ම රාශි - E හා H - තරංගයේ මාර්ගය නිරුපණය කරන ඛණ්ඩාංකය දිගේ පමණක් විචලනය වන්නකි. මෙය = ඛණ්ඩාංකය ලෙස ගන්න. මේ රාශිවල සංචරක අතුරින් -අක්ෂයට ලම්බ තලවල පිහිටන ඒවායේ අගය නියත වෙයි.

(5) සමීකරණයෙන්

අපසා E

Eගේ සංරචක -අක්ෂය දිගේත් -අක්ෂය දිගේත් විචලනය ‍නොවන බැවින්

එබැවින්

එහෙත් මේ සලකා බලනුයේ තරංගයේ මාර්ගය - එනම් X−අක්ෂය — දිගේ දෛශිකයන් විචලනය වන තරංග චලිතයකි. එබැවින් ඉහත දැක්වූ ප්‍රතිඵලය අනුව = 0

(6) සමීකරණය උපකල්පනය කිරීමෙන් බව ද එමෙන් ම පෙන්විය හැකිය. එවිට ඉතිරි වන්නේ Eගේත් Hගේත් සංචරක අතුරෙන් —අක්ෂයට ලම්බ -එනම් තරංග ප්‍රචාරණ දිශාව එල්ලේ වූ- ඒවායි.

එබැවින් E හා H අතර අපසරණය ශූන්‍ය යැ යන කරුණ අනුව තල තරංගය තිර්යක් බව නිගමනය වෙයි.

E සහ E සංචරක සඳහා මේ සමීකරණය වෙයි:

.....(12)

චුම්බක දෛශිකයේ සංචරක සඳහා ද මෙවැනි ම සමීකරණ ලැබේ.

E හා H සඳහා එක විසඳුම් කාණ්ඩයක් මෙසේ ලිවිය හැකියි.

සඳහා විසැඳුම් කාණ්ඩයක් මෙසේයි.

..............(15)

..............(16)

මෙහි නිරූපණය කරන්නේ තරංග චලිතයේ ආවර්තයයි; A, B නියතයෝයි.

තල-ධ්‍රැවිත තරංග

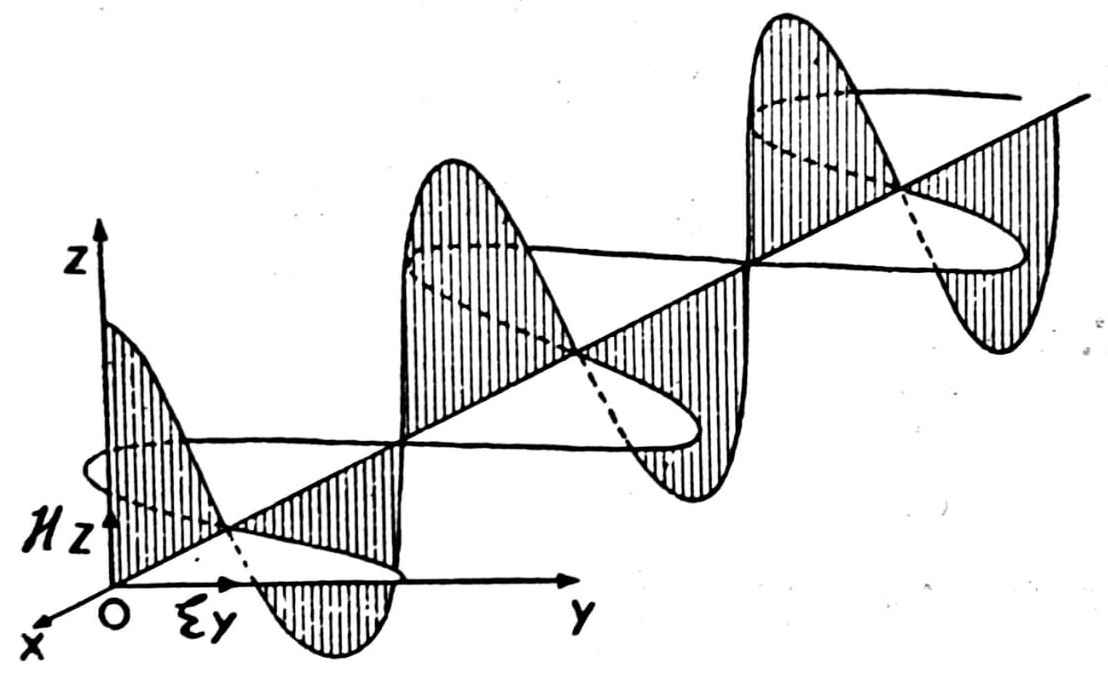
EZ = HY = O යැයි සිතන්න. තරංග පෙරමුණෙහි එකකට එකක් සෘජු කෝණික ව අචල දිශා එල්ලේ පිහිටන E සහ H සහිත ඒකවර්ණ තල තරංගයක් (13), (14) සමීකරණවලින් නිරූපණය වෙයි. එවැනි තරංගයට තල-ධ්‍රැවිතයැයි කියනු ලැබේ.

එවැනි තරංගයෙක ක්ෂණික සටහනක් පහත පෙනෙන ප්‍රස්තාරාත්මක රූපය දක්වයි.

HZ චුම්බක දෛශිකය ඇතුළත් වන XOZ තලය ධ්‍රැවණ තලය නම් වේ.

විද්‍යුත්චුම්බක තරංගවල ප්‍රවේගය

(9), (10) සමීකරණවලින් නිරූපණය වුණු විද්‍යුත්චුම්බක තරංගවල ප්‍රවේගය

යන්නෙන් ලැබෙන බව පෙනී ගියේය.

අබාධ අවකාශයේ = = 1. එබැවින් ආරෝපණයේ ස්.වි.ඒට වි.චු.ඒ. දක්වන අනුපාතය වන ට මෙම තරංගවල ප්‍රවේගය සමානය. අබාධ අවකාශය සඳහා ත් ත් පිළිබඳ සමකාලීන නිර්ණයන දෙකක් අනුව පහත දැක්වෙන අගය ලැබී තිබේ.

පරීක්ෂණ දෝෂ සීමා සලකන කල මේ අගය එකක් අනෙක හා සීහෙයි.

එසේ වුව ද ද්‍රව්‍ය තුළ දී සාමාන්‍යයෙන් ට වඩා වෙනස්ය. පාරදෘශ්‍ය ද්‍රව්‍ය බොහොමයක ට ආසන්නය.

එබැවින්

ද්‍රව්‍යයේ වර්තනාංකය = , එනම් ද්‍රව්‍යය තුළ දී ආලෝකයේ ප්‍රවේගයට රික්තයෙක දී ආලෝකයේ ප්‍රවේගය දක්වන අනුපාතයයි.

මෙසේ

හෙවත් අන් අයුරෙකින් පවසතොත් පාරවිද්‍යුත් නියතයේ වර්ග මූලයට වර්තනාංකය සමානය.

වර්ණාවලියේ මැද සඳහා වූ අගය භාවිත කිරීමෙන් මේ ප්‍රතිඵල ලැබිණි:

වාතය

හයිඩ්රජන්

කාබන්ඩයොක්සයිඩ්

එහෙත් ද්‍රව්‍ය බොහොමයක් සඳහා වෙනස අධික ය. මේ අනුව ජලය සඳහා = . වර්තනාංක නිර්ණය කරනුයේ ඉතා ශීඝ්‍රයෙන් ප්‍රතිවර්ත වන ක්ෂේත්‍ර සහිත ආලෝක තරංග සඳහාය. එහෙත් සාමාන්‍යයෙන් පාරවිද්‍යුත් නියත නිර්ණය කරනුයේ ස්ථාවර ක්ෂේත්‍ර සඳහාය. වෙනසට හේතුව මෙය බව සොයා ගෙන ඇත.

විද්‍යුත් චුම්බක තරංගවල ශක්තිය

ද්‍රව්‍යමය වස්තු විද්‍යුත්චුම්බක ක්ෂේත්‍ර හා අන්‍යෝන්‍ය ක්‍රියාකාරිත්වයට පැමිණීමේ දී එම වස්තු වැඩිපුර ශක්තිය ලබාගැනීම හෝ ශක්තියෙන් හීනවීම හෝ සාමාන්‍ය ස්වභාවයයි. එබැවින් ශක්ති සංස්ථිතිය පිළිබඳ නියමය රැකගැනීමට නම් විද්‍යුත්චුම්බක ක්ෂේත්‍රය ම ශක්තියේ මූලස්ථානය බව උපකල්පනය කළ යුතුය. මේ ශක්තිය ඒකක පරිමාවට බැගින් ක්ෂේත්‍රය පුරා පැතිරී සිටින්නේ යැයි සිතා ගත හැකි ය.

තල විද්‍යුත්චුම්බක තරංගයක් සඳහා

බව (13), (14) සමීකරණවලින් පෙනී යයි.

මේ නිසා තල තරංගයක් සඳහා බව පෙනේ.

මෙසේ මේ අවස්ථාවේ දී ශක්තියෙන් අඩක් විද්‍යුත් ශක්තියයි. අඩක් චුම්බක ශක්තියයි.

සැම විද්‍යුත්චුම්බක තරංගයක් ම ශක්තිය ගෙන යන බව දන්නා කරුණකි.

තරංග යන ප්‍රවේගයෙකින් ඉදිරියට යන්නේ යැයි උපකල්පනය කිරීමෙන්, ප්‍රචාරණ දිශාවට ලම්බ පෘෂ්ඨයෙක ඒකක වර්ග ඵලයක් හරහා කාලයක් තුළ ගලන ශක්ති ප්‍රමාණය ගණනය කළ හැකිය. මෙය හරස්කඩ වර්ගඵලය සෙමී. ක් වූ ද උස v. 8 වූ ද පරිමාවෙහි, — එනම් පරිමාවෙක — අන්තර්ගත ශක්ති ප්‍රමාණයට සමානය.

මෙසේ =

එබැවින් තලයේ තල-ධ්‍රැවිත වූ ද දිශාවට ගමන් කරන්නාවූ ද තල විද්‍යුත්චුම්බක තරංගයෙක, ප්‍රචාරණය දිශාවට ලම්බ ඒකක වර්ගඵලයක් හරහා ගලා යන ශක්තිය යන්නෙන් දැක්වේ.

මේ අනුව ඕනෑ ම තල තරංගයෙක ගලා යන ශක්තිය ප්‍රචාරණ දිශාවට එල්ල වූ දෛශිකයෙකින් නිරූපණය කළ හැකි ය. එහි විශාලත්වය යන්නෙන් දැක් වේ. මෙය පොයිටිං දෛශිකයයි.

E හා H යනු කාලයේ ආවර්ත ශ්‍රිත බැවින් ඕනෑම තැනෙක පොයිටිං දෛශිකයේ අගය ශුන්‍යයත් උපරිම අගයකුත් අතර ආවර්ත ලෙස විචලනය වෙයි. එහෙත් Eත් Hත් සැම විට ම කලාවෙන් සම බැවින් ඒ අගයේ ලකුණ—එනම් එහි දිශාව—සැම විට එක ම වෙයි.

විද්‍යුත්චුම්බක තරංගවල ගම්‍යතාව

විද්‍යුත් චුම්බක ක්ෂේත්‍රයන් හා අන්‍යොන්‍ය ක්‍රියකාරිත්වයට පැමිණි ද්‍රව්‍යමය වස්තූන්ගේ ගම්‍යතාව ද වෙනස් වී යන බව පෙනී ගොස් ඇත. එබැවින් ගම්‍යතාවේත් කෝණික ගම්‍යතාවේත් මූලධර්ම රැක ගනු වස් ගම්‍යතාව ද විද්‍යුත්චුම්බක ක්ෂේත්‍රයට අයිති බව සැලැකීම අවශ්‍යය.

මේ විද්‍යුත්චුම්බක ගම්‍යතාව දෛශික රාශියකි. එය ක්ෂේත්‍රයේ ඕනෑම තැනෙක දී පොයිටිං දෛශිකය දිශාවට ක්‍රියා කරයි. අබාධ අවකාශයේ දී ඒකක පරිමාවෙක විද්‍යුත්චුම්බක ගම්‍යතාව, න් බෙදූ පොයිටිං දෛශිකයට සම බව පෙන්විය හැකිය. අන් ඕනෑ ම මාධ්‍යයෙක දී එය ගුණ කළ පොයිංටිං දෛශිකයට සම වෙයි. මෙසේ විද්‍යුත් චුම්බක තරංග, ශක්තිය පමණක් නොව ගම්‍යතාව ද ගෙන යයි.

ඉහතින් විස්තර කළ වර්ගයේ තල-ධ්‍රැවිත තරංගයෙක ඒකක පරිමාවක ගම්‍යතා ප්‍රමාණය

විද්‍යුත්චුම්බක තරංග ගම්‍යතාව ගෙන යන්නේ යැ යන කරුණ වටිනා ප්‍රතිඵල රැසක් ම ලබා දෙයි. ඒ අතුරින් ඉතා ම වැදගත් යැයි සැලැකිය හැක්ක නම් ආලෝකයත් එවැනි වෙනත් විකිරණත් ද්‍රව්‍යමය වස්තු මත පීඩනයක් මෙහෙයැවීමට සමත් යැ යන කරුණයි. සුප්‍රකට විකිරණ පීඩනය යනු මේ යැ.

මේ විකිරණ පීඩනය සඳහා සෛද්ධාන්තික ගණනයෙන් ලත් විශාලත්වයන්ගේ නිවැරදි බව පරීක්ෂණාත්මක ප්‍රතිඵල මඟින් මොනවට ඔප්පු වී ඇත.

විද්‍යුත්චුම්බක වාදයේ වෙනත් ප්‍රතිඵල

ආලෝකයේ අනෙක් ප්‍රකට ගුණ බොහොමයක් පැහැදිලි කිරීමට පිළිවන් වූයේ මැක්ස්වෙල්ගේ ගණිතමය වාදය නිසාය.

ආලෝකයේ පරාවර්තනය, වර්තනය, ප්‍රකිරණය යන සංසිද්ධි පමණක් නොව ධ්‍රැවණය හා සම්බන්ධ සංසිද්ධි ගණනාවක් ම සාර්ථක අන්දමින් තේරුම් කරන ලද්දේ එකී වාදයෙනි. සමසාර්වදිශ මාධ්‍යවල මෙන් ම අසමසාර්වදිශ මාධ්‍යවලත් සන්නායක මාධ්‍යවල මෙන්ම අබාධ අවකාශයේත් ආලෝකය හැසිරෙන සැටි ද ඉන් නිගමනය කරන ලදි.

(කර්තෘ: ඔස්මන්ඩ් ජයරත්න)

(සංස්කරණය: 1965)